
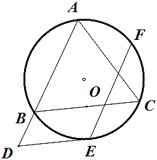
【题目】如图,△ABC内接于⊙O,AB=AC=10,BC=12,点E是弧BC的中点.
(1)过点E作BC的平行线交AB的延长线于点D,求证:DE是⊙O的切线.
(2)点F是弧AC的中点,求EF的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接AE,由等弦对等弧可得![]() ,进而推出
,进而推出![]() ,可知AE为⊙O的直径,再由等腰三角形三线合一得到AE⊥BC,根据DE∥BC即可得DE⊥AE,即可得证;
,可知AE为⊙O的直径,再由等腰三角形三线合一得到AE⊥BC,根据DE∥BC即可得DE⊥AE,即可得证;
(2)连接BE,AF,OF,OF与AC交于点H,AE与BC交于点G,利用勾股定理求出AG,然后求直径AE,再利用垂径定理求出HF,最后用勾股定理求AF和EF.
证明:(1)如图,连接AE,
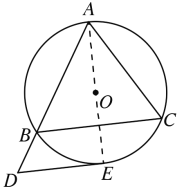
∵AB=AC
∴![]()
又∵点E是弧BC的中点,即![]()
∴![]() ,即
,即![]()
∴AE为⊙O的直径,
∵![]()
∴∠BAE=∠CAE
又∵AB=AC
∴AE⊥BC
∵DE∥BC
∴DE⊥AE
∴DE是⊙O的切线.
(2)如图,连接BE,AF,OF,OF与AC交于点H,AE与BC交于点G,
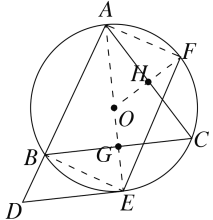
∴∠ABE=∠AFE=90°,OF⊥AC
由(1)可知AG垂直平分BC,∴BG=![]() BC=6
BC=6
在Rt△ABG中,![]()
∵cos∠BAE=cos∠BAG
∴![]() ,即
,即![]()
∴AE=![]()
∴⊙O的直径为![]() ,半径为
,半径为![]() .
.
设HF=x,则OH=![]()
∴在Rt△AHO中,![]()
即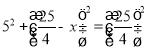 ,
,
解得![]()
∴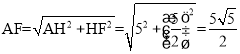
∴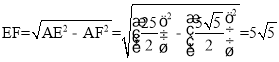


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像经过两点
的图像经过两点![]() 、
、![]() .
.
(1)如果![]() 、
、![]() 、
、![]() 都是整数,且
都是整数,且![]() ,求
,求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)设二次函数![]() 的图像与
的图像与![]() 轴的交点为
轴的交点为![]() 、
、![]() ,与
,与![]() 轴的交点为
轴的交点为![]() .如果关于
.如果关于![]() 的方程
的方程![]() 的两个根都是整数,求
的两个根都是整数,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(4,3),B(3,1),C(1,2),△A1B1C1与△ABC关于原点对称.
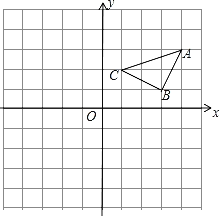
(1)写出A1,B1,C1的坐标;
(2)在所给的平面直角坐标系中画出△A1B1C1;
(3)若点A(4,3)与点M(a﹣2,b﹣4)关于原点对称,求关于x的方程![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置,...,则正方形铁片连续旋转2019次后,点P的坐标为________
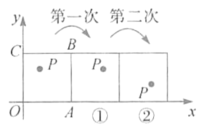
查看答案和解析>>
科目:初中数学 来源: 题型:
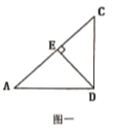
【题目】如图,在![]() 中,过点
中,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,垂足分别为
,垂足分别为![]() .连接
.连接![]() 交线段
交线段![]() 于点
于点![]() .
.
(1)在图一![]() 中,
中,![]() ,
,![]() ,有几组相似的三角形,请写出来;
,有几组相似的三角形,请写出来;
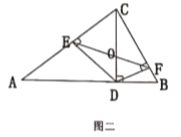
(2)在图二中,证明:![]() ;
;
(3)如果![]() ,
,![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
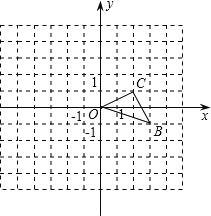
【题目】如图,已知O是坐标原点,B,C两点的坐标分别为(3,﹣1),(2,1).
(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍,画出图形;
(2)分别写出B,C两点的对应点B′,C′的坐标;
(3)求△OB′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
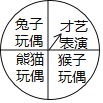
【题目】某校举行“元旦”联欢晚会,其中有一个转转盘抽奖环节,有两名幸运观众分别转动如图所示的转盘各一次(转盘被分成四个相等的扇形区域,分别写有“兔子玩偶”、“熊猫玩偶”、“猴子玩偶”、“才艺表演”),转盘停止后(指针指在分界线时重转),若指针指向某种玩偶,则获得相应的玩偶,若指针指向才艺表演,则要在舞台上进行才艺表演且没有任何奖品,小娟和小寒是这两名幸运观众,用树状图或列表的方法求小娟和小寒均要进行才艺表演的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com