
【题目】公司以10元/千克的价格收购一批产品进行销售,经过市场调查获悉,日销售量y(千克)是销售价格x(元/千克)的一次函数,部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)直接写出y与x之间的函数表达式;
(2)求日销售利润为150元时的销售价格;
(3)若公司每销售1千克产品需另行支出a元(0<a<10)的费用,当20≤x≤25时,公司的日获利润的最大值为1215元,求a的值.
【答案】(1)y=﹣15x+450;(2)销售价格为(20+3![]() )元或(20﹣3
)元或(20﹣3![]() )元;(3)a的值为2
)元;(3)a的值为2
【解析】
(1)设一次函数解析式为y=kx+b(≠0),任选两点求表达式,求得k便可;
(2)根据题意列出日销售利润w与销售价格x之间的函数关系式,根据二次函数的性质确定最大值即可;
(3)根据题意列出日销售利润w与销售价格x之间的函数关系式,依据二次函数的最大值列出a的一元二次方程求得a的值.
解:(1)设一次函数解析式为y=kx+b(≠0),
把x=10,y=300和x=20,y=150代入得
![]()
解得:![]() ,
,
∴y=﹣15x+450;
(2)设日销售利润w=y(x﹣10)=(﹣15x+450)(x﹣10)
即w=﹣15x2+600x﹣4500,
当w=150时,150=﹣15x2+600x﹣4500,
解得,![]()
答:日销管利润为150元时的销售价格为(![]() )元或(
)元或(![]() )元;
)元;
(3)日获利w=y(x﹣10﹣a)=(﹣15x+450)(x﹣10﹣a),
即w=﹣15x2+(600+15a)x﹣(450a+4500),
对称轴为![]() ,
,
∵0<a<10,
∴![]() ,
,
∴当![]() 时,w有最大值,为w
时,w有最大值,为w![]() ,
,
解得a1=2,a2=38>10(舍去),
综上所述,a的值为2.
故答案是:(1)y=﹣15x+450;(2)销售价格为(20+3![]() )元或(20﹣3
)元或(20﹣3![]() )元;(3)a的值为2
)元;(3)a的值为2


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.

(1)在旋转过程中,
①当A,D,M三点在同一直线上时,求AM的长.
②当A,D,M三点为同一直角三角形的顶点时,求AM的长.
(2)若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2,如图2,此时∠AD2C=135°,CD2=60,求BD2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定:把一次函数y=kx+b的一次项系数和常数项互换得y=bx+k,我们称y=kx+b和y=bx+k(其中k·b≠0,且|k|≠|b|))为互助一次函数,例如:y=-2x+3和y=3x-2就是互助一次函数.如图1所示,一次函数y=kx+b和它的互助一次函数的图象![]() 1,
1,![]() 2交于点P,
2交于点P,![]() 1,
1,![]() 2与x轴、y轴分别交于点A,B和点C,D.
2与x轴、y轴分别交于点A,B和点C,D.
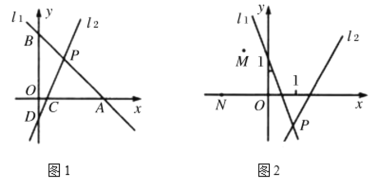
(1)如图1所示,当k=-1,b=5时,直接写出点P的坐标是_________.
(2)如图2所示,已知点M(-1,1.5),N(-2,0).试探究随着k,b值的变化,MP+NP的值是否发生变化,若不变,求出MP+NP的值;若变化,求出使MP+NP取最小值时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店以每件50元的价格购进![]() 两种服装,已知销售30件
两种服装,已知销售30件![]() 种服装和40件
种服装和40件![]() 种服装共获利润1000元,销售40件
种服装共获利润1000元,销售40件![]() 种服装和50件
种服装和50件![]() 种服装共获利润1300元.
种服装共获利润1300元.
(1)求两种服装每件的售价;
(2)若该服装店准备购进![]() 两种服装共80件,并规定
两种服装共80件,并规定![]() 种服装不少于
种服装不少于![]() 种服装的
种服装的![]() ,设购进
,设购进![]() 种服装
种服装![]() 件,求利润
件,求利润![]() (元)与
(元)与![]() (件)之间的函数解析式,并求出当
(件)之间的函数解析式,并求出当![]() 取何值时,利润最大,最大利润为多少?
取何值时,利润最大,最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P,已知BC=6,AH=4.当矩形DEFG面积最大时,HP的长是( )
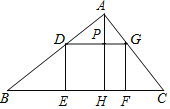
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
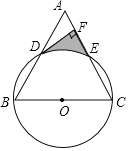
【题目】已知:如图,以等边△ABC的边BC为直径作⊙O,分别交AB,AC于点D,E,过点D作DF⊥AC交AC于点F.
(1)求证:DF是⊙O的切线;
(2)若等边△ABC的边长为8,求由![]() 、DF、EF围成的阴影部分面积.
、DF、EF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“机动车行驶到斑马线要礼让行人”等交通法规实施后,某校数学课外实践小组对这些交通法规的了解情况在全校随机调查了部分学生,调查结果分为四种:A.非常了解,B.比较了解,C.基本了解,D.不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
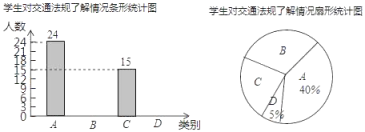
请结合图中所给信息解答下列问题:
(1)本次共调查 名学生;扇形统计图中C所对应扇形的圆心角度数是 ;
(2)补全条形统计图;
(3)学校准备从组内的甲、乙、丙、丁四位学生中随机抽取两名学生参加市区交通法规竞赛,请用列表或画树状图的方法求丙和丁两名学生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD、BC于E、F点,连结CE,若OC![]() cm,CD=4cm,则DE的长为( )
cm,CD=4cm,则DE的长为( )
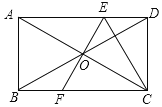
A.![]() cmB.5cmC.3cmD.2cm
cmB.5cmC.3cmD.2cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com