
 如图,ABCD为正方形,E是BC边上一点,将正方形折叠,使A点与E点重合,折痕为MN.如果tan∠AEN=$\frac{1}{3}$,DC+CE=10,那么△ANE的面积为$\frac{10}{3}$.
如图,ABCD为正方形,E是BC边上一点,将正方形折叠,使A点与E点重合,折痕为MN.如果tan∠AEN=$\frac{1}{3}$,DC+CE=10,那么△ANE的面积为$\frac{10}{3}$. 分析 由翻折变换的性质得出∠AEN=∠EAN,然后先由tan∠AEN=$\frac{1}{3}$,可得出BE=$\frac{1}{3}$AB,然后DC+CE=10可知BE=2,从而得到AB=6,然后再Rt△ABE中,由勾股定理可求得BN的长,最后依据三角形的面积公式求解即可.
解答 解:由翻折的性质可知:∠AEN=∠EAN.
∵tan∠AEN=$\frac{1}{3}$,
∴tan∠BAE=$\frac{1}{3}$.
∴AB=3BE.
∵EC+CD=10,
∴6BE-BE=10.
解得:BE=2.
∴AB=6.
∴${S}_{△ABE}=\frac{1}{2}×2×6$=6.
设AN=EN=x,则BN=6-x.
在Rt△NBE中,由勾股定理可知:BE2+BN2=NE2,即(6-x)2=x2+22.
解得:x=$\frac{8}{3}$.
∴BN=$\frac{8}{3}$.
∴${S}_{△BNE}=\frac{1}{2}×2×\frac{8}{3}$=$\frac{8}{3}$.
∴S△ANE=S△ABE-S△BNE=6-$\frac{8}{3}$=$\frac{10}{3}$.
故答案为:$\frac{10}{3}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用、三角形的面积公式,依据勾股定理列出关于x的方程是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
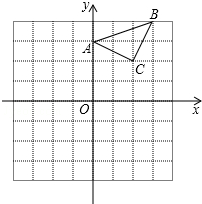 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com