
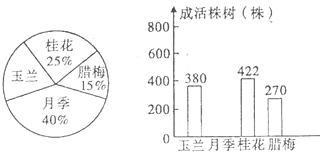
【题目】“不出城郭而获山水之怡,身居闹市而有林泉之致”,合肥市某区不断推进“园林城市”建设,今春种植了四类花苗,园林部门从种植的这批花苗中随机抽取了2000株,将四类花苗的种植株数绘制成扇形统计图,将四类花苗的成活株数绘制成条形统图.经统计这批2000株的花苗总成活率为90%,其中玉兰和月季的成活率较高,根据图表中的信息解答下列问题:
(1)扇形统计图中玉兰所对的圆心角为 ,并补全条形统计图;
(2)该区今年共种植月季8000株,成活了约 株;
(3)园林部门决定明年从这四类花苗中选两类种植,请用列表法或画树状图求恰好选到成活率较高的两类花苗的概率.
【答案】(1)72°,见解析;(2)7280;(3)![]() .
.
【解析】
(1)根据题意列式计算,补全条形统计图即可;
(2)根据题意列式计算即可;
(3)画树状图得出所有等可能的情况数,找出选到成活率较高的两类树苗的情况数,即可求出所求的概率.
(1)扇形统计图中玉兰所对的圆心角为360°×(1-40%-15%-25%)=72°
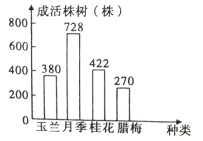
月季的株数为2000×90%-380-422-270=728(株),
补全条形统计图如图所示:
(2)月季的成活率为![]()
所以月季成活株数为8000×91%=7280(株).
故答案为:7280.
(3)由题意知,成活率较高的两类花苗是玉兰和月季,玉兰、月季、桂花、腊梅分别用A、B、C、D表示,画树状图如下:
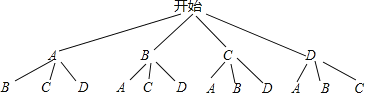
所有等可能的情况有12种,其中恰好选到成活率较高的两类花苗有2种.
∴P(恰好选到成活率较高的两类花苗)![]()


科目:初中数学 来源: 题型:
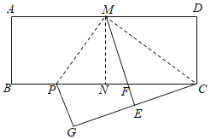
【题目】如图,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() 交
交![]() 于点
于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() 垂直平分
垂直平分![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的是( )
.其中正确的是( )
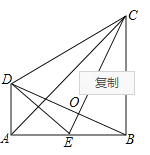
A.①②③B.①③⑤C.①②④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,将矩形
,将矩形![]() 对折,得到折痕
对折,得到折痕![]() ;沿着
;沿着![]() 折叠,点
折叠,点![]() 的对应点为
的对应点为![]() 与
与![]() 的交点为
的交点为![]() ;再沿着
;再沿着![]() 折叠,使得
折叠,使得![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ,此时点
,此时点![]() 的对应点为
的对应点为![]() .下列结论:①
.下列结论:①![]() 是直角三角形:②点
是直角三角形:②点![]() 在同一条直线上;③
在同一条直线上;③![]() ;④
;④![]() ;⑤点
;⑤点![]() 是
是![]() 的外心,其中正确的个数为( )
的外心,其中正确的个数为( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm,点P为边AC上一点,且AP=5cm.点Q为边AB上的任意一点(不与点A,B重合),若点A关于直线PQ的对称点A'恰好落在△ABC的边上,则AQ的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推进生态文明建设,甲、乙两工程队同时为崂山区的两条绿化带铺设草坪.两队所铺设草坪的面积![]() (米)与施工时间
(米)与施工时间![]() (时)之间关系的近似可以用此图象描述.请结合图象解答下列问题:
(时)之间关系的近似可以用此图象描述.请结合图象解答下列问题:
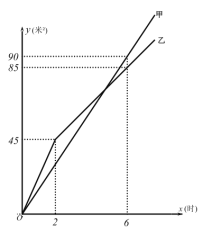
(1)从工作2小时开始,施工方从乙队抽调两人对草坪进行灌溉,乙队速度有所降低,求乙队在工作2小时后![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)求乙队降速后,何时铺设草坪面积为甲队的![]() ?
?
(3)乙队降速后,甲乙两队铺设草坪速度之比为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
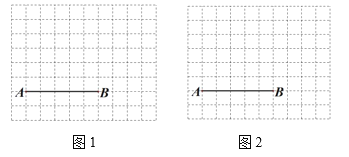
【题目】图1、图2分别是![]() 的网格,网格中每个小正方形的边长均为1,
的网格,网格中每个小正方形的边长均为1,![]() 、
、![]() 两点在小正方形的顶点上,请在图1、图2中各取一点
两点在小正方形的顶点上,请在图1、图2中各取一点![]() (点
(点![]() 必须在小正方形的顶点上),使以
必须在小正方形的顶点上),使以![]() 、
、![]() 、
、![]() 为顶点的三角形分别满足以下要求:
为顶点的三角形分别满足以下要求:
(1)在图1中画一个![]() ,使
,使![]() 是以
是以![]() 为斜边的直角三角形,且
为斜边的直角三角形,且![]() ;
;
(2)在图2中画一个![]() ,使
,使![]() 为等腰三角形,且
为等腰三角形,且![]() ,直接写出
,直接写出![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx-3a-5经过点A(2,5)
(1)求出a和b之间的数量关系.
(2)已知抛物线的顶点为D点,直线AD与y轴交于(0,-7)
①求出此时抛物线的解析式;
②点B为y轴上任意一点且在直线y=5和直线y=-13之间,连接BD绕点B逆时针旋转90°,得到线段BC,连接AB、AC,将AB绕点B顺时针旋转90°,得到线段BH.截取BC的中点F和DH的中点G.当点D、点H、点C三点共线时,分别求出点F和点G的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com