
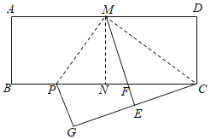
【题目】如图,在矩形![]() 中,
中,![]() ,将矩形
,将矩形![]() 对折,得到折痕
对折,得到折痕![]() ;沿着
;沿着![]() 折叠,点
折叠,点![]() 的对应点为
的对应点为![]() 与
与![]() 的交点为
的交点为![]() ;再沿着
;再沿着![]() 折叠,使得
折叠,使得![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ,此时点
,此时点![]() 的对应点为
的对应点为![]() .下列结论:①
.下列结论:①![]() 是直角三角形:②点
是直角三角形:②点![]() 在同一条直线上;③
在同一条直线上;③![]() ;④
;④![]() ;⑤点
;⑤点![]() 是
是![]() 的外心,其中正确的个数为( )
的外心,其中正确的个数为( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】D
【解析】
根据折叠的性质得到∠DMC=∠EMC,∠AMP=∠EMP,于是得到∠PME+∠CME=![]() ×180°=90°,求得△CMP是直角三角形,故①正确;根据平角的定义得到点C、E、G在同一条直线上,故②正确;AB=1,则AD=2
×180°=90°,求得△CMP是直角三角形,故①正确;根据平角的定义得到点C、E、G在同一条直线上,故②正确;AB=1,则AD=2![]() ,得到DM=
,得到DM=![]() AD=
AD=![]() ,根据勾股定理得到CM=
,根据勾股定理得到CM=![]() =
=![]() ,根据射影定理得到CP=
,根据射影定理得到CP=![]() =
=![]() ,得到PC=
,得到PC=![]() MP,故③正确;求得PB=
MP,故③正确;求得PB=![]() AB=
AB=![]() ,
,![]() ,故④正确;根据平行线等分线段定理得到CF=PF,求得点F是△CMP外接圆的圆心,故⑤正确.
,故④正确;根据平行线等分线段定理得到CF=PF,求得点F是△CMP外接圆的圆心,故⑤正确.
∵沿着CM折叠,点D的对应点为E,
∴∠DMC=∠EMC,
∵再沿着MP折叠,使得AM与EM重合,折痕为MP,
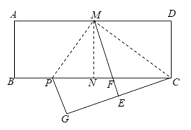
∴∠AMP=∠EMP,
∵∠AMD=180°,
∴∠PME+∠CME=![]() ×180°=90°,
×180°=90°,
∴△CMP是直角三角形;故①正确;
∵沿着CM折叠,点D的对应点为E,
∴∠D=∠MEC=90°,
∵再沿着MP折叠,使得AM与EM重合,折痕为MP,
∴∠MEG=∠A=90°,
∴∠GEC=180°,
∴点C、E、G在同一条直线上,故②正确;
∵AD=2![]() AB,
AB,
∵AB=1,则AD=2![]() ,
,
∵将矩形ABCD对折,得到折痕MN;
∴DM=![]() AD=
AD=![]()
∴CM=![]() =
=![]() ,
,
∵∠PMC=90°,MN⊥PC,
∴CM2=CNCP,
∴CP=![]() =
=![]() ,
,
∴PN=CPCN=![]()
∴PM=![]() =
=![]()
∴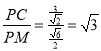 ,
,
∴PC=![]() MP,故③正确;
MP,故③正确;
∵PC=![]() AB=
AB=![]() ,
,
∴PB=![]() -
-![]() =
=![]()
∴![]() ,故④正确,
,故④正确,
∵CD=CE,EG=AB,AB=CD,
∴CE=EG,
∵∠CEM=∠G=90°,
∴FE∥PG,
∴CF=PF,
∵∠PMC=90°,
∴CF=PF=MF,
∴点F是△CMP外接圆的圆心,故⑤正确;
故选:D.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
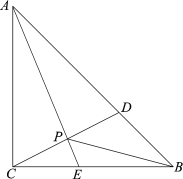
【题目】如图,在△ABC中,AE平分∠BAC交BC于点E,D是AB边上一动点,连接CD交AE于点P,连接BP.已知AB =6cm,设B,D两点间的距离为xcm,B,P两点间的距离为y1cm,A,P两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,![]() ),并画出函数y1,
),并画出函数y1,![]() 的图象;
的图象;

(3)结合函数图象,回答下列问题:
①当AP=2BD时,AP的长度约为 cm;
②当BP平分∠ABC时,BD的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
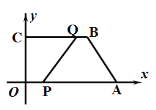
【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0),A(12,0),B(8,6),C(0,6).动点P从点O出发,以每秒3个单位长度的速度沿边OA向终点A运动;动点Q从点B同时出发,以每秒2个单位长度的速度沿边BC向终点C运动.设运动的时间为t秒,作AG⊥PQ于点G,则AG的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.6
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一动点,过
上一动点,过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,将
,将![]() 折叠得到
折叠得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
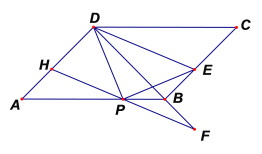
(1)求证:![]() ;
;
(2)当![]() 时,证明
时,证明![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
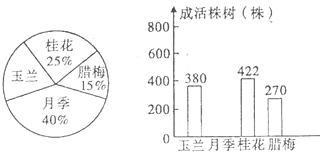
【题目】“不出城郭而获山水之怡,身居闹市而有林泉之致”,合肥市某区不断推进“园林城市”建设,今春种植了四类花苗,园林部门从种植的这批花苗中随机抽取了2000株,将四类花苗的种植株数绘制成扇形统计图,将四类花苗的成活株数绘制成条形统图.经统计这批2000株的花苗总成活率为90%,其中玉兰和月季的成活率较高,根据图表中的信息解答下列问题:
(1)扇形统计图中玉兰所对的圆心角为 ,并补全条形统计图;
(2)该区今年共种植月季8000株,成活了约 株;
(3)园林部门决定明年从这四类花苗中选两类种植,请用列表法或画树状图求恰好选到成活率较高的两类花苗的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A的坐标是A(x,y),从1、2、3这三个数中任取一个数作为x的值,再从余下的两个数中任取一个数作为y的值.则点A落在直线y=﹣x+5与直线y=![]() x及y轴所围成的封闭区域内(含边界)的概率是_____.
x及y轴所围成的封闭区域内(含边界)的概率是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com