
【题目】点A的坐标是A(x,y),从1、2、3这三个数中任取一个数作为x的值,再从余下的两个数中任取一个数作为y的值.则点A落在直线y=﹣x+5与直线y=![]() x及y轴所围成的封闭区域内(含边界)的概率是_____.
x及y轴所围成的封闭区域内(含边界)的概率是_____.
科目:初中数学 来源: 题型:
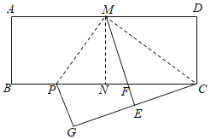
【题目】如图,在矩形![]() 中,
中,![]() ,将矩形
,将矩形![]() 对折,得到折痕
对折,得到折痕![]() ;沿着
;沿着![]() 折叠,点
折叠,点![]() 的对应点为
的对应点为![]() 与
与![]() 的交点为
的交点为![]() ;再沿着
;再沿着![]() 折叠,使得
折叠,使得![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ,此时点
,此时点![]() 的对应点为
的对应点为![]() .下列结论:①
.下列结论:①![]() 是直角三角形:②点
是直角三角形:②点![]() 在同一条直线上;③
在同一条直线上;③![]() ;④
;④![]() ;⑤点
;⑤点![]() 是
是![]() 的外心,其中正确的个数为( )
的外心,其中正确的个数为( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx-3a-5经过点A(2,5)
(1)求出a和b之间的数量关系.
(2)已知抛物线的顶点为D点,直线AD与y轴交于(0,-7)
①求出此时抛物线的解析式;
②点B为y轴上任意一点且在直线y=5和直线y=-13之间,连接BD绕点B逆时针旋转90°,得到线段BC,连接AB、AC,将AB绕点B顺时针旋转90°,得到线段BH.截取BC的中点F和DH的中点G.当点D、点H、点C三点共线时,分别求出点F和点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区为了加强社区居民对新型冠状病非肺炎防护知识的了解,通过微信群宣传新型冠状病毒肺炎的防护知识,并鼓励社区居民在线参与作答《2020年新型冠状病毒防治全国统一考试(全国卷)》试卷,社区管理员随机从甲、乙两个小区各抽取![]() 名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
名人员的答卷成绩,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:![]()
![]()
乙小区:![]()
![]()
整理数据
成绩 |
|
|
|
|
甲小区 |
|
|
|
|
乙小区 |
|
|
|
|
分析数据
统计量 | 平均数 | 中位教 | 众数 |
甲小区 |
|
|
|
乙小区 |
|
|
|
应用数据
(1)填空:![]() _ _;
_ _;
(2)若甲小区共有![]() 人参与答卷,请估计甲小区成绩大于
人参与答卷,请估计甲小区成绩大于![]() 分的人数;
分的人数;
(3)社区管理员看完统计数据,认为甲小区对新型冠状病毒肺炎防护知识掌握更好,请你写出社区管理员的理由(至少写出一条) .
查看答案和解析>>
科目:初中数学 来源: 题型:
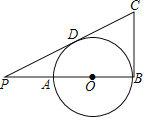
【题目】如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
A.1.5B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学小组对函数y1=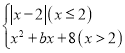 图象和性质进行探究.当x=4时,y1=0.
图象和性质进行探究.当x=4时,y1=0.
(1)当x=5时,求y1的值;
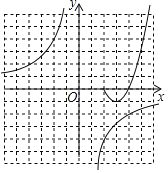
(2)在给出的平面直角坐标系中,补全这个函数的图象,并写出这个函数的一条性质;
(3)进一步探究函数图象并解决问题:已知函数y2=﹣![]() 的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.
的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
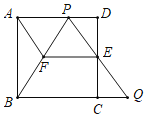
【题目】如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:![]() ;
;
(2)过点E作![]() 交PB于点F,连结AF,当
交PB于点F,连结AF,当![]() 时,①求证:四边形AFEP是平行四边形;
时,①求证:四边形AFEP是平行四边形;
②请判断四边形AFEP是否为菱形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与
与![]() 铀交于
铀交于![]() ,与
,与![]() 轴交于
轴交于![]() 抛物线的顶点为
抛物线的顶点为![]() 直线
直线![]() 过
过![]() 交
交![]() 轴于
轴于![]() .
.
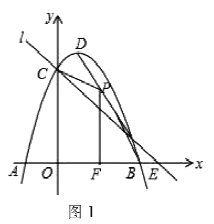
(1)写出![]() 的坐标和直线
的坐标和直线![]() 的解析式;
的解析式;
(2)![]() 是线段
是线段![]() 上的动点(不与
上的动点(不与![]() 重合),
重合),![]() 轴于
轴于![]() 设四边形
设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的两数关系式,并求
之间的两数关系式,并求![]() 的最大值;
的最大值;
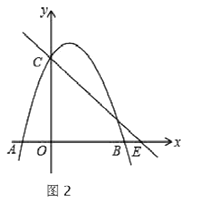
(3)点![]() 在
在![]() 轴的正半轴上运动,过
轴的正半轴上运动,过![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于
于![]() 交抛物线于
交抛物线于![]() 连接
连接![]() ,将
,将![]() 沿
沿![]() 翻转,
翻转,![]() 的对应点为
的对应点为![]() .在图2中探究:是否存在点
.在图2中探究:是否存在点![]() ;使得
;使得![]() 恰好落在
恰好落在![]() 轴?若存在,请求出
轴?若存在,请求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com