
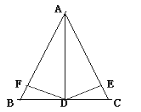
【题目】如图:在△ABC中,AD是∠BAC的平分线,DE⊥AC于E,DF⊥AB于F,且FB=CE,则下列结论:①DE=DF,②AE=AF,③BD=CD,④AD⊥BC。
其中正确的有___________ (填序号)。
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
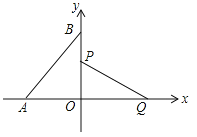
【题目】如图,已知Rt△OBA,∠ABO=30°,OA=2,两条直角边重叠在互相的垂直的两条直线上,线段PQ的端点P从点O出发,沿△OBA的边按O→B→A→O运动一周,同时另一端点Q随之在直线AO上运动,如果PQ=![]() ,那么当点P运动一周时,点Q运动的总路程为____________.
,那么当点P运动一周时,点Q运动的总路程为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为3,F为BC边上的动点,FD⊥AB于D,FE⊥AC于E,则DE的长为( )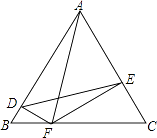
A.随F点运动,其值不变
B.随F点运动而变化,最大值为 ![]()
C.随F点运动而变化,最小值为 ![]()
D.随F点运动而变化,最小值为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
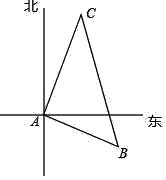
【题目】如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度的比为4:3,货船沿东偏南10°方向航行,2小时后货船到达B处,客船到达C处,若此时两船相距50海里.
(1)求两船的速度分别是多少?
(2)求客船航行的方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系。
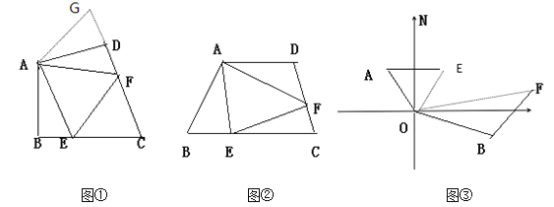
(1)小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,即可得出BE,EF,FD之间的数量关系,他的结论应是____________。
象上面这样有公共顶点,锐角等于较大角的一半,且组成这个较大角的两边相等的几何模型称为半角模型。
(2)拓展 如图②,若在四边形ABCD中,,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF=![]() ∠BAD,则BE,EF,FD之间的数量关系是________________。
∠BAD,则BE,EF,FD之间的数量关系是________________。
请证明你的结论。
(3)实际应用 如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西35°的A处,舰艇乙在指挥中心南偏东75°的B处,,且两舰艇到指挥中心的距离相等接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为65°,试求此时两舰艇之间的距离是_____________海里 (直接写出答案)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=12,BC=8,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF= . 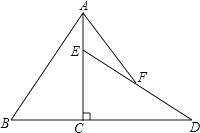
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
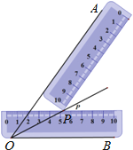
A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 三角形三条垂直平分线的交点到三个定点的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知双曲线y=![]() (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,4),则△AOC的面积为( )
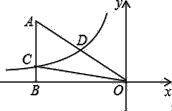
A. 6 B. 12 C. 18 D. 24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com