
【题目】计算:
(1)化简: ![]()
(2)解不等式组,并求其最小整数解.  .
.
【答案】
(1)解: ![]()
= ![]()
![]()
= ![]()
![]()
= ![]()
(2)解: 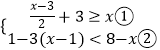 ,
,
解①得:x≤3,
解②得:x>﹣2,
故不等式组的解集为:﹣2<x≤3,
故不等式的最小整数解为:﹣1
【解析】(1)先将1看作是![]() ,然后依据通分母分式的减法法则计算括号内的减法,接下来,将分式的分子分母进行分解,最后进行约分即可;
,然后依据通分母分式的减法法则计算括号内的减法,接下来,将分式的分子分母进行分解,最后进行约分即可;
(2)先求得两个不等式的解集,然后再,依据大小小大中间找出确定出不等式组的解集,最后,再找出符合条件的整数解即可.
【考点精析】利用分式的混合运算和一元一次不等式组的解法对题目进行判断即可得到答案,需要熟知运算的顺序:第一级运算是加法和减法;第二级运算是乘法和除法;第三级运算是乘方.如果一个式子里含有几级运算,那么先做第三级运算,再作第二级运算,最后再做第一级运算;如果有括号先做括号里面的运算.如顺口溜:"先三后二再做一,有了括号先做里."当有多层括号时,先算括号内的运算,从里向外{[(?)]};解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的盒子,甲盒子中装有3张卡片,卡片上分别写着3cm、7cm、9cm;乙盒子中装有4张卡片,卡片上分别写着2cm、4cm、6cm、8cm;盒子外有一张写着5cm的卡片.所有卡片的形状、大小都完全相同.现随机从甲、乙两个盒子中各取出一张卡片,与盒子外的卡片放在一起,用卡片上标明的数量分别作为一条线段的长度.
(1)请用树状图或列表的方法求这三条线段能组成三角形的概率;
(2)求这三条线段能组成直角三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,面积为6cm2的△ABC纸片沿BC方向平移至△DEF的位置,平移的距离是BC长的2倍,则△ABC纸片扫过的面积为( )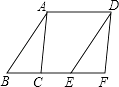
A.18cm2
B.21cm2
C.27cm2
D.30cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
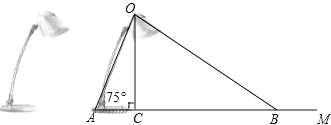
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26, ![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.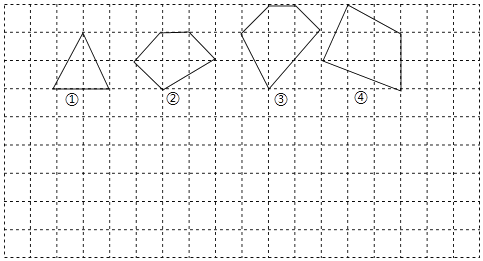
(1)根据图中提供的信息填表:
格点多边形各边上的 | 格点边多边形内部的 | 格点多边形的面积 | |
多边形1 | 4 | 1 | 2 |
多边形2 | 5 | 2 | ② |
多边形3 | 6 | 3 | 5 |
多边形4 | ① | 4 |
|
一般格点多边形 | m | n | S |
则S=(用含m、n的代数式表示)
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=(用含m、n的代数式表示).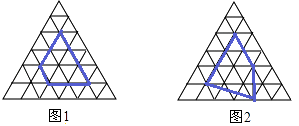
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com