
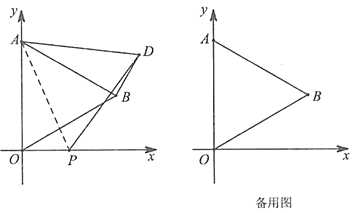
【题目】如图,在平面直角坐标系中,已知![]() 是等边三角形,点
是等边三角形,点![]() 的坐标是(0,4),点
的坐标是(0,4),点![]() 在第一象限,点
在第一象限,点![]() 是
是![]() 轴上的一个动点,连接
轴上的一个动点,连接![]() ,并把
,并把![]() 绕点
绕点![]() 按逆时针方向旋转,使边
按逆时针方向旋转,使边![]() 与
与![]() 重合.连接
重合.连接![]() ,
,![]() ,得
,得![]() .
.
(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)在点![]() 运动过程中,依照条件所形成的
运动过程中,依照条件所形成的![]() 面积为
面积为![]() .
.
①当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②当t≤0时,要使![]() ,请直接写出所有符合条件的点
,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
【答案】(1)DP=![]() ;(2)①
;(2)① ;②P(
;②P(![]() ,0),P(
,0),P(![]() ,0),P(
,0),P(![]() ,0).
,0).
【解析】
(1)由△ABD由△AOP旋转得到,利用旋转的性质得到两三角形全等,利用全等三角形对应边相等,对应角相等得到AP=AD,∠DAB=∠PAO,进而得到三角形ADP为等边三角形,根据A点坐标及t的值利用勾股定理求出AP的长即可得答案;(2)①过点![]() ,
,![]() 分别作
分别作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,过点
,过点![]() 作
作![]() 轴的平行线,分别交
轴的平行线,分别交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,由等边三角形的性质可得
,由等边三角形的性质可得![]() ,根据∠ABD=90°可求出∠DBG=60°,利用∠DBG的正弦函数可求出DG的长,即可得DH的长,利用三角形面积公式即可得答案;②分两种情况:当P在x轴负半轴,但D在x轴上方时.即
,根据∠ABD=90°可求出∠DBG=60°,利用∠DBG的正弦函数可求出DG的长,即可得DH的长,利用三角形面积公式即可得答案;②分两种情况:当P在x轴负半轴,但D在x轴上方时.即![]() <t≤0时,方法同①类似,也是在直角三角形DBG用BD的长表示出BG,进而求出GF的长,然后利用面积公式列方程求出t值即可;当P在x轴负半轴;D在x轴下方时,即t≤
<t≤0时,方法同①类似,也是在直角三角形DBG用BD的长表示出BG,进而求出GF的长,然后利用面积公式列方程求出t值即可;当P在x轴负半轴;D在x轴下方时,即t≤![]() 时,过B作BE⊥y轴,过D作DH⊥x轴,交BE延长线于G,在Rt△BDG中,用BD的长表示出DG,进而得出DH的长,根据面积公式列方程求出t值即可,综上即可得答案.
时,过B作BE⊥y轴,过D作DH⊥x轴,交BE延长线于G,在Rt△BDG中,用BD的长表示出DG,进而得出DH的长,根据面积公式列方程求出t值即可,综上即可得答案.
(1)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是由
是由![]() 旋转得到,
旋转得到,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)①当![]() 时,如图,
时,如图,![]() ,
,
过点![]() ,
,![]() 分别作
分别作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,过点
,过点![]() 作
作![]() 轴的平行线,分别交
轴的平行线,分别交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,
,
∵![]() 为等边三角形,
为等边三角形,![]() 轴,
轴,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴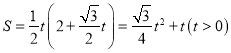 ;
;
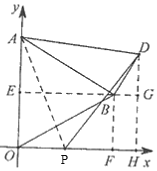
②如图,当P在x轴负半轴,但D在x轴上方时.即![]() <t≤0时,过点
<t≤0时,过点![]() ,
,![]() 分别作
分别作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,过点
,过点![]() 作
作![]() 轴的平行线,分别交
轴的平行线,分别交![]() 轴于点
轴于点![]() ,过D作DG⊥BF,交BF于点
,过D作DG⊥BF,交BF于点![]() ,
,
∵∠ABE=30°,∠ABD=90°,BF⊥BE,
∴∠DBG=30°,
∵BD=OP=-t,
∴BG=BD![]() cos30°=-
cos30°=-![]() t,
t,
∵BF=OE=2,
∴DH=GF=BF-BG=2+![]() t,
t,
∴S=![]()
![]() OP
OP![]() DH=
DH=![]() ×(-t)×(2+
×(-t)×(2+![]() t)=
t)=![]() ,
,
解得:t1=![]() ,t2=
,t2=![]() ,
,
∴P点坐标为(![]() ,0)或(
,0)或(![]() ,0).
,0).

当D在x轴下方时,即t≤![]() 时,过B作BE⊥y轴,过D作DH⊥x轴,交BE延长线于G,
时,过B作BE⊥y轴,过D作DH⊥x轴,交BE延长线于G,
∵∠ABE=30°,∠ABD=90°,DG⊥BG,
∴∠BDG=30°,
∵BD=OP=-t,
∴DG=BD![]() cos30°=-
cos30°=-![]() t,
t,
∵GH=OE=2,
∴DH=DG-GH=-![]() t-2,
t-2,
∴S=![]()
![]() OP
OP![]() DH=
DH=![]() ×(-t)×(-
×(-t)×(-![]() t-2)=
t-2)=![]() ,
,
解得:t1=![]() ,t2=
,t2=![]() (舍去),
(舍去),
∴P点坐标为(![]() ,0).
,0).
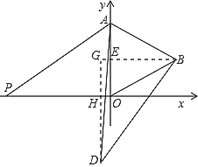
综上所述:符合条件的点![]() 的坐标为(
的坐标为(![]() ,0)或(
,0)或(![]() ,0)或(
,0)或(![]() ,0).
,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:初中数学 来源: 题型:
【题目】小张去文具店购买作业本,作业本有大、小两种规格,大本作业本的单价比小本作业本贵0.3元,已知用8元购买大本作业本的数量与用5元购买小本作业本的数量相同.
(1)求大本作业本与小本作业本每本各多少元?
(2)因作业需要,小张要再购买一些作业本,购买小本作业本的数量是大本作业本数量的2倍,总费用不超过15元.则大本作业本最多能购买多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P是BA延长线上一点,过点P作⊙O的切线PC,切点是C,过点C作弦![]() 于E,连接CO,CB.
于E,连接CO,CB.
(1)求证:PD是⊙O的切线;
(2)若![]() ,
,![]() ,求PA的长;
,求PA的长;
(3)试探究线段AB,OE,OP之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实视力保护工作,某校组织七年级学生开展了视力保健活动.活动前随机测查了30名学生的视力,活动后再次测查这部分学生的视力.两次相关数据记录如下:
活动前被测查学生视力数据:
(1)4.0 4.1 4.1 4.2 4.2 4.3 4.3 4.4 4.4 4.4 4.5 4.5 4.6 4.6 4.6
(2)4.7 4.7 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 5.0 5.0 5.1
活动后被测查学生视力数据:
(2)4.0 4.2 4.3 4.4 4.4 4.5 4.5 4.6 4.6 4.6 4.7 4.7 4.7 4.7 4.8
(3)4.8 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 4.9 4.9 5.0 5.0 5.1 5.1
活动后被测查学生视力频数分布表
分组 | 频数 |
| 1 |
| 2 |
| b |
| 7 |
| 12 |
| 4 |
根据以上信息回答下列问题:
(1)填空:![]() ______,
______,![]() ______,活动前被测查学生视力样本数据的中位数是______,活动后被测查学生视力样本数据的众数是______;
______,活动前被测查学生视力样本数据的中位数是______,活动后被测查学生视力样本数据的众数是______;
(2)若视力在4.8及以上为达标,估计七年级600名学生活动后视力达标的人数有多少?
(3)分析活动前后相关数据,从一个方面评价学校开展视力保健活动的效果.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组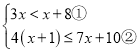 .请结合题意填空,完成本题的解答:
.请结合题意填空,完成本题的解答:
(1)解不等式①,得:________;
(2)解不等式②,得:________;
(3)把不等式①和②的解集在数轴上表示出来:
![]()
(4)原不等式组的解集为:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平面图形![]() ,点
,点![]() 、
、![]() 是
是![]() 上任意两点,我们把线段
上任意两点,我们把线段![]() 的长度的最大值称为平面图形
的长度的最大值称为平面图形![]() 的“宽距”.例如,正方形的宽距等于它的对角线的长度.
的“宽距”.例如,正方形的宽距等于它的对角线的长度.
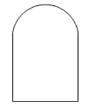
(1)写出下列图形的宽距:
①半径为![]() 的圆:________;
的圆:________;
②如图,上方是半径为![]() 的半圆,下方是正方形的三条边的“窗户形“:________;
的半圆,下方是正方形的三条边的“窗户形“:________;
(2)如图,在平面直角坐标系中,已知点![]() 、
、![]() ,
,![]() 是坐标平面内的点,连接
是坐标平面内的点,连接![]() 、
、![]() 、
、![]() 所形成的图形为
所形成的图形为![]() ,记
,记![]() 的宽距为
的宽距为![]() .
.
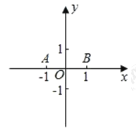
①若![]() ,用直尺和圆规画出点
,用直尺和圆规画出点![]() 所在的区域并求它的面积(所在区域用阴影表示);
所在的区域并求它的面积(所在区域用阴影表示);
②若点![]() 在⊙
在⊙![]() 上运动,⊙
上运动,⊙![]() 的半径为
的半径为![]() ,圆心
,圆心![]() 在过点
在过点![]() 且与
且与![]() 轴垂直的直线上.对于⊙
轴垂直的直线上.对于⊙![]() 上任意点
上任意点![]() ,都有
,都有![]() ,直接写出圆心
,直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中有两个小岛![]() ,
,![]() ,某渔船在海中的
,某渔船在海中的![]() 处测得小岛D位于东北方向上,且相距
处测得小岛D位于东北方向上,且相距![]() ,该渔船自西向东航行一段时间到达点
,该渔船自西向东航行一段时间到达点![]() 处,此时测得小岛
处,此时测得小岛![]() 恰好在点
恰好在点![]() 的正北方向上,且相距
的正北方向上,且相距![]() ,又测得点
,又测得点![]() 与小岛
与小岛![]() 相距
相距![]() .
.
(1)求![]() 的值;
的值;
(2)求小岛![]() ,
,![]() 之间的距离(计算过程中的数据不取近似值).
之间的距离(计算过程中的数据不取近似值).

查看答案和解析>>
科目:初中数学 来源: 题型:
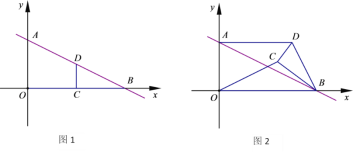
【题目】如图,在平面直角坐标系中,直线l:![]() 与x轴.y轴交于B,A两点,点D,C分别为线段AB,OB的中点,连结CD,如图,将△DCB绕点B按顺时针方向旋转角
与x轴.y轴交于B,A两点,点D,C分别为线段AB,OB的中点,连结CD,如图,将△DCB绕点B按顺时针方向旋转角![]() ,如图.
,如图.
(1)连结OC,AD,求证![]() ∽
∽![]() ;
;
(2)当0°<![]() <180°时,若△DCB旋转至A,C,D三点共线时,求线段OD的长;
<180°时,若△DCB旋转至A,C,D三点共线时,求线段OD的长;
(3)试探索:180°<![]() <360°时,是否还有可能存在A,C,D三点共线的情况,若存在,求出此直线的表达式;若不存在,请说明理由.
<360°时,是否还有可能存在A,C,D三点共线的情况,若存在,求出此直线的表达式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校落实新课改精神的情况,现以该校九年级二班的同学参加课外活动的情况为样本,对其参加“球类”、“绘画类”、“舞蹈类”、“音乐类”、“棋类”活动的情况进行调查统计,并绘制了如图所示的统计图.
(1)参加音乐类活动的学生人数为 人,参加球类活动的人数的百分比为 ;
(2)请把图2(条形统计图)补充完整;
(3)该校学生共600人,则参加棋类活动的人数约为 ;
(4)该班参加舞蹈类活动的4位同学中,有1位男生(用E表示)和3位女生(分别用F,G,H表示),先准备从中选取两名同学组成舞伴,请用列表或画树状图的方法求恰好选中一男一女的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com