
����Ŀ����֪ƽ��ͼ��![]() ����
����![]() ��
��![]() ��
��![]() ���������㣬���ǰ��߶�
���������㣬���ǰ��߶�![]() �ij��ȵ����ֵ��Ϊƽ��ͼ��
�ij��ȵ����ֵ��Ϊƽ��ͼ��![]() �ġ����ࡱ�����磬�����εĿ���������ĶԽ��ߵij��ȣ�
�ġ����ࡱ�����磬�����εĿ���������ĶԽ��ߵij��ȣ�
��1��д������ͼ�εĿ��ࣺ
�ٰ뾶Ϊ![]() ��Բ��________��
��Բ��________��
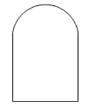
����ͼ���Ϸ��ǰ뾶Ϊ![]() �İ�Բ���·��������ε������ߵġ������Ρ���________��
�İ�Բ���·��������ε������ߵġ������Ρ���________��
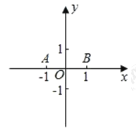
��2����ͼ����ƽ��ֱ������ϵ�У���֪��![]() ��
��![]() ��
��![]() ������ƽ���ڵĵ㣬����
������ƽ���ڵĵ㣬����![]() ��
��![]() ��
��![]() ���γɵ�ͼ��Ϊ
���γɵ�ͼ��Ϊ![]() ����
����![]() �Ŀ���Ϊ
�Ŀ���Ϊ![]() ��
��
����![]() ����ֱ�ߺ�Բ�滭����
����ֱ�ߺ�Բ�滭����![]() ���ڵ����������������������������Ӱ��ʾ����
���ڵ����������������������������Ӱ��ʾ����
������![]() �ڡ�
�ڡ�![]() ���˶�����
���˶�����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() ��Բ��
��Բ��![]() �ڹ���
�ڹ���![]() ����
����![]() �ᴹֱ��ֱ���ϣ����ڡ�
�ᴹֱ��ֱ���ϣ����ڡ�![]() �������
�������![]() ������
������![]() ��ֱ��д��Բ��
��ֱ��д��Բ��![]() �ĺ�����
�ĺ�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
���𰸡���1����1����![]() ����2�������Ϊ2���ڵ�
����2�������Ϊ2���ڵ�![]() �ĺ�����ķ�ΧΪ
�ĺ�����ķ�ΧΪ![]() ��
��
��������
��1����ƽ��ͼ��![]() �ġ����ࡱ�Ķ��弴�ɽ�����⣮
�ġ����ࡱ�Ķ��弴�ɽ�����⣮
����ͼ��������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() �����Բ��Բ��Ϊ
�����Բ��Բ��Ϊ![]() ����
����![]() �ǡ�
�ǡ�![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��
��![]() �����
�����![]() �����ֵ���ɽ�����⣮
�����ֵ���ɽ�����⣮
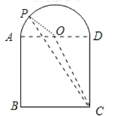
��2������ͼ2��1�У���![]() ���ڵ�������ͼ��������
���ڵ�������ͼ��������![]() �����Ϊ
�����Ϊ![]() ��
��
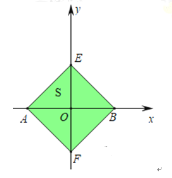
����ͼ2��2�У�����![]() ��
��![]() ����Ҳ�ʱ������
����Ҳ�ʱ������![]() ����
����![]() ����
����![]() �����
�����![]() ��
��![]() ʱ����
ʱ����![]() �����꣬�����жϣ��ٸ��ݶԳ��������
�����꣬�����жϣ��ٸ��ݶԳ��������![]() ��
��![]() ���������μ��ɣ�
���������μ��ɣ�
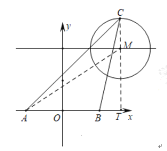
��1���ٰ뾶Ϊ![]() ��Բ�Ŀ�����Ϊ
��Բ�Ŀ�����Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��
����ͼ��������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() �����Բ��Բ��Ϊ
�����Բ��Բ��Ϊ![]() ����
����![]() �ǡ�
�ǡ�![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��
��![]() ��
��
��![]() ��
�У�![]()
![]()
![]() ��
��
![]()
![]() ��
��
![]() ����������Ρ��Ŀ���Ϊ
����������Ρ��Ŀ���Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��
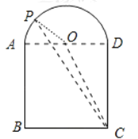
��2������ͼ����![]() ���ڵ�������ͼ��������
���ڵ�������ͼ��������![]() �����Ϊ2��
�����Ϊ2��
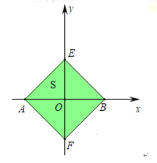
����ͼ������![]() ��
��![]() ����Ҳ�ʱ������
����Ҳ�ʱ������![]() ����
����![]() ����
����![]() ��
��
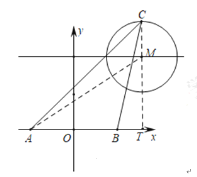
![]()
![]() ����
����![]()
![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() ��
��
![]()
![]() ����ʱ
����ʱ![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
![]()
![]() ����ʱ
����ʱ![]() ��
��
![]() ���������ĵ�
���������ĵ�![]() �ĺ�����ķ�ΧΪ
�ĺ�����ķ�ΧΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
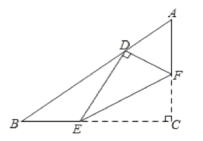
����Ŀ����ͼ,��Rt��ABC��,��C=90����AC=3��BC=4����E��F�ֱ��ڱ�BC��AC�ϣ���EF���ڵ�ֱ���۵���C��ʹ��C�Ķ�Ӧ��Dǡ�����ڱ�AB�ϣ�����EFC�͡�ABC���ƣ���AD�ij�Ϊ___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016�꣬ijƶ�����ļ�ͥ���˾�������Ϊ2500Ԫ��ͨ��������ҵ���֣���չ����ֳҵ��2018�꣬��ͥ���˾�������ﵽ��3600Ԫ��
��1�����ƶ����2016�굽2018���ͥ���˾����������ƽ�������ʣ�
��2������ƽ�������ʱ��ֲ��䣬2019���ƶ�����ļ�ͥ���˾��������Ƿ��ܴﵽ4200Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c(a<0)������(-1,0)��������4a+2b+c>0.���½���(1)a+b>0;(2)a+c>0;(3)-a+b+c>0;(4)b2-2ac>5a2������ȷ�ĸ�����( )
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
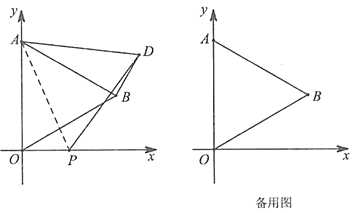
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪![]() �ǵȱ������Σ���
�ǵȱ������Σ���![]() ��������(0��4)����
��������(0��4)����![]() �ڵ�һ���ޣ���
�ڵ�һ���ޣ���![]() ��
��![]() ���ϵ�һ�����㣬����
���ϵ�һ�����㣬����![]() ������
������![]() �Ƶ�
�Ƶ�![]() ����ʱ�뷽����ת��ʹ��
����ʱ�뷽����ת��ʹ��![]() ��
��![]() �غϣ�����
�غϣ�����![]() ��
��![]() ����
����![]() ��
��
(1)��![]() ʱ����
ʱ����![]() �ij���
�ij���
(2)�ڵ�![]() �˶������У������������γɵ�
�˶������У������������γɵ�![]() ���Ϊ
���Ϊ![]() ��
��
�ٵ�![]() ʱ����
ʱ����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
�ڵ�t��0ʱ��Ҫʹ![]() ����ֱ��д�����з��������ĵ�
����ֱ��д�����з��������ĵ�![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ�����![]() ��
��
��1����֤�����κ�����ͼ����x�����������㣻
��2�������κ�����ͼ����x�����������ĺ������Ϊ��������aΪ������ʱ����a��ֵ�����κ����Ľ���ʽ���������κ�����ͼ�����б���ֻҪ��������x�����������A��B��A��B����ࣩ����y��Ľ���C���䶥��D���ĵ㻭�����κ����Ĵ���ͼ��ͬʱ���A��B��C��D��λ�ã���
��3���ڣ�2���������£����κ�����ͼ�����Ƿ����һ��Pʹ![]() ��������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�
��������ڣ������P�����ꣻ��������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
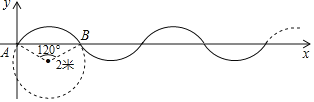
����Ŀ����ͼ���ڵ�λ����Ϊ1��ƽ��ֱ������ϵ�У��������ɰ뾶Ϊ2�ף�Բ�Ľ�Ϊ![]() ��
��![]() ��θ��Ʋ���β���Ӷ��ɣ�����һ��P��A(AΪ����ԭ��)��������ÿ��
��θ��Ʋ���β���Ӷ��ɣ�����һ��P��A(AΪ����ԭ��)��������ÿ��![]() ���ٶ������������˶������ڵ�2019��ʱ��P��������Ϊ( )
���ٶ������������˶������ڵ�2019��ʱ��P��������Ϊ( )
A. ��2B. ��1C. 0D. 1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
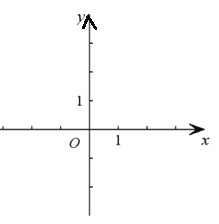
����Ŀ����ƽ��ֱ������ϵxOy��(��ͼ)����֪������y��x2��2x���䶥��ΪA.
(1)д�����������ߵĿ��ڷ�����A�����꣬��˵�����ı仯�����
(2)���ǰ�һ���������Ϻ���������������ȵĵ�������������ߵġ������㡱
������������y��x2��2x�ġ������㡱�����ꣻ
��ƽ��������y��x2��2x��ʹ�����������ߵĶ���B�Ǹ������ߵġ������㡱����Գ�����x�ύ�ڵ�C�����ı���OABC�����Σ����������ߵı���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=��x+4��ͼ���뷴����![]() ��kΪ��������k��0����ͼ����A��1��a����B��b��1�����㣬
��kΪ��������k��0����ͼ����A��1��a����B��b��1�����㣬

��1�����������ı���ʽ����A��B������
��2����x������һ�㣬ʹPA+PB��ֵ��С�������������ĵ�P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com