
【题目】如图,海中有两个小岛![]() ,
,![]() ,某渔船在海中的
,某渔船在海中的![]() 处测得小岛D位于东北方向上,且相距
处测得小岛D位于东北方向上,且相距![]() ,该渔船自西向东航行一段时间到达点
,该渔船自西向东航行一段时间到达点![]() 处,此时测得小岛
处,此时测得小岛![]() 恰好在点
恰好在点![]() 的正北方向上,且相距
的正北方向上,且相距![]() ,又测得点
,又测得点![]() 与小岛
与小岛![]() 相距
相距![]() .
.
(1)求![]() 的值;
的值;
(2)求小岛![]() ,
,![]() 之间的距离(计算过程中的数据不取近似值).
之间的距离(计算过程中的数据不取近似值).

科目:初中数学 来源: 题型:
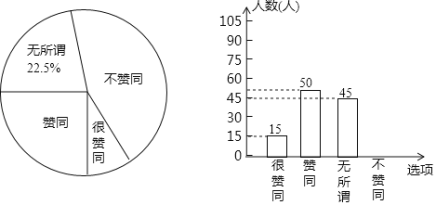
【题目】某校调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图,根据图中提供的信息,完成以下问题:
(1)本次共调查了 名家长,扇形统计图中“很赞同”所对应的圆心角度数是 度,并补全条形统计图.
(2)该校共有3600名家长,通过计算估计其中“不赞同”的家长有多少名?
(3)从“不赞同”的五位家长中(两女三男),随机选取两位家长对全校家长进行“学生使用手机危害性”的专题讲座,请用树状图或列表法求出选中“1男1女”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
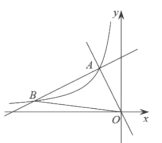
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 和
和![]() 的图象相交于点
的图象相交于点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求反比例函数的表达式;
(2)设一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象的另一个交点为
的图象的另一个交点为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
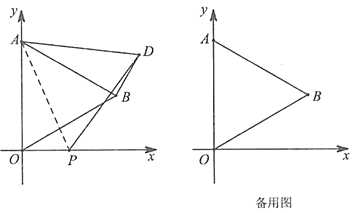
【题目】如图,在平面直角坐标系中,已知![]() 是等边三角形,点
是等边三角形,点![]() 的坐标是(0,4),点
的坐标是(0,4),点![]() 在第一象限,点
在第一象限,点![]() 是
是![]() 轴上的一个动点,连接
轴上的一个动点,连接![]() ,并把
,并把![]() 绕点
绕点![]() 按逆时针方向旋转,使边
按逆时针方向旋转,使边![]() 与
与![]() 重合.连接
重合.连接![]() ,
,![]() ,得
,得![]() .
.
(1)当![]() 时,求
时,求![]() 的长;
的长;
(2)在点![]() 运动过程中,依照条件所形成的
运动过程中,依照条件所形成的![]() 面积为
面积为![]() .
.
①当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
②当t≤0时,要使![]() ,请直接写出所有符合条件的点
,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
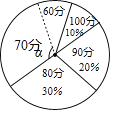
【题目】某校有20名同学参加市举办的“文明环保,从我做起”征文比赛,成绩分别记为60分、70分、80分、90分、100分,为方便奖励,现统计出80分、90分、100分的人数,制成如图不完整的扇形统计图,设70分所对扇形圆心角为α.
(1)若从这20份征文中,随机抽取一份,则抽到试卷的分数为低于80分的概率是 ;
(2)当![]() 时,求成绩是60分的人数;
时,求成绩是60分的人数;
(3)设80分为唯一众数,求这20名同学的平均成绩的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在单位长度为1米的平面直角坐标系中,曲线是由半径为2米,圆心角为![]() 的
的![]() 多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒
多次复制并首尾连接而成.现有一点P从A(A为坐标原点)出发,以每秒![]() 米的速度沿曲线向右运动,则在第2019秒时点P的纵坐标为( )
米的速度沿曲线向右运动,则在第2019秒时点P的纵坐标为( )
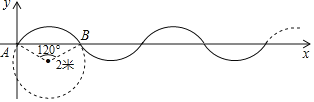
A. ﹣2B. ﹣1C. 0D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
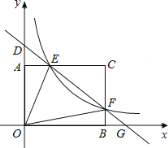
【题目】如图,矩形AOBC的顶点坐标分别为A(0,3),O(0,0),B(4,0),C(4,3),动点F在边BC上(不与B.C重合),过点F的反比例函数y=![]() 的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为
的图象与边AC交于点E,直线EF分别与y轴和x轴相交于点D和G.给出下列命题:①若k=4,则△OEF的面积为![]() ;②若k=
;②若k=![]() ,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=
,则点C关于直线EF的对称点在x轴上;③满足题设的k的取值范围是0<k≤12;④若DEEG=![]() ,则k=1.其中正确的命题的序号是____________(填序号).
,则k=1.其中正确的命题的序号是____________(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
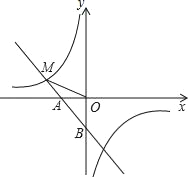
【题目】如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数![]() 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)当y2>y1时,求x的取值范围;
(3)求点B到直线OM的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
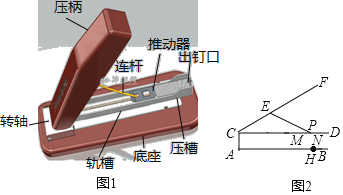
【题目】如图1是某品牌订书机,其截面示意图如图2所示.订书钉放置在轨槽CD内的MD处,由连接弹簧的推动器MN推紧,连杆EP一端固定在压柄CF上的点E处,另一端P在DM上移动.当点P与点M重合后,拉动压柄CF会带动推动器MN向点C移动.使用时,压柄CF的端点F与出钉口D重合,纸张放置在底座AB的合适位置下压完成装订(即点D与点H重合).已知CA⊥AB,CA=2cm,AH=12cm,CE=5cm,EP=6cm,MN=2cm.
(1)求轨槽CD的长(结果精确到0.1);
(2)装入订书钉需打开压柄FC,拉动推动器MN向点C移动,当∠FCD=53°时,能否在ND处装入一段长为2.5cm的订书钉?(参考数据:![]() ≈2.24,
≈2.24,![]() ≈6.08,sin53°≈0.80,cos53°≈0.60)
≈6.08,sin53°≈0.80,cos53°≈0.60)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com