
【题目】如图,已知一次函数 y=kx-2 的图象与 x 轴、y 轴分别交于 A,B 两点,与反比例函数![]() 的图象交于点 C,且 AB=AC,则 k 的值为( )
的图象交于点 C,且 AB=AC,则 k 的值为( )
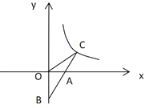
A.1B.2C.3D.4
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中有两点![]() 、
、![]() ,我们定义
,我们定义![]() 、
、![]() 两点间的“
两点间的“![]() 值”直角距离为
值”直角距离为![]() ,且满足
,且满足![]() ,其中
,其中![]() .小静和佳佳在解决问题:(求点
.小静和佳佳在解决问题:(求点![]() 与点
与点![]() 的“1值”直角距离
的“1值”直角距离![]() )时,采用了两种不同的方法:
)时,采用了两种不同的方法:
(方法一):![]() ;
;
(方法二):如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作直线
作直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]()
请你参照以上两种方法,解决下列问题:
(1)已知点![]() ,点
,点![]() ,则
,则![]() 、
、![]() 两点间的“2值”直角距离
两点间的“2值”直角距离![]() .
.
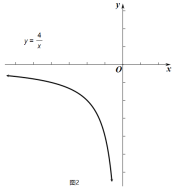
(2)函数![]() 的图像如图2所示,点
的图像如图2所示,点![]() 为其图像上一动点,满足
为其图像上一动点,满足![]() 两点间的“
两点间的“![]() 值”直角距离
值”直角距离![]() ,且符合条件的点
,且符合条件的点![]() 有且仅有一个,求出符合条件的“
有且仅有一个,求出符合条件的“![]() 值”和点
值”和点![]() 坐标.
坐标.
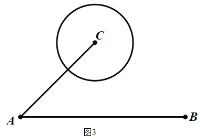
(3)城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走,因此,两地之间修建垂直和平行的街道常常转化为两点间的“![]() 值”直角距离,
值”直角距离,![]() 地位于
地位于![]() 地的正东方向上,
地的正东方向上,![]() 地在
地在![]() 点东北方向上且相距
点东北方向上且相距![]() ,以
,以![]() 为圆心修建了一个半径为
为圆心修建了一个半径为![]() 的圆形湿地公园,现在要在公园和
的圆形湿地公园,现在要在公园和![]() 地之间修建观光步道.步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元,问:修建这一规光步道至少要多少万元?
地之间修建观光步道.步道只能东西或者南北走向,并且东西方向每千米成本是20万元,南北方向每千米的成本是10万元,问:修建这一规光步道至少要多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
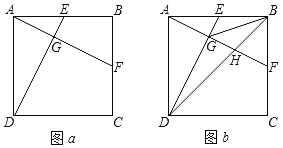
【题目】如图a,在正方形ABCD中,E、F分别为边AB、BC的中点,连接AF、DE交于点G.
(1)求证:AF⊥DE;
(2)如图b,连接BG,BD,BD交AF于点H.
①求证:GB2=GAGD;
②若AB=10,求三角形GBH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6080元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现:
如图 1,在边长为 1 小的正方形网格中,连接格点 A、B 和 C、D,AB 和 CD 相交于点 P,求 tan ∠CPB 的值方法归纳:求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形,观察发现问题中∠ CPB不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点 B、 E,可得 BE∥CD,则∠ABE=∠CPB,连接AE,那么∠CPB 就变换到 Rt△ABE 中.问题解决:
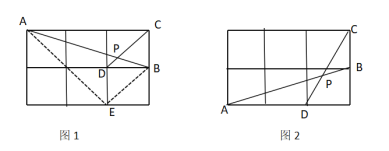
(1)直接写出图 1 中 tan CPB 的值为______;
(2)如图 2,在边长为 1 的正方形网格中,AB 与 CD 相交于点 P,求 cos CPB 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
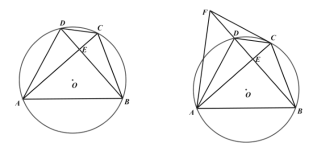
【题目】四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
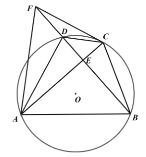
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人加工同一种零件,甲每天加工的数量是乙每天加工数量的 1.5 倍,两人各加工 600 个这种零件,甲比乙少用 5 天.
(1)求甲、乙两人每天各加工多少个这种零件?
(2)已知甲、乙两人加工这种零件每天的加工费分别是 150 元和 120 元,现有 3000 个这种零件的加工任务,甲单独加工一段时间后另有安排,剩余任务由乙单独完成.如果总加工费不超过 7800 元,那么甲至少加工了多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com