
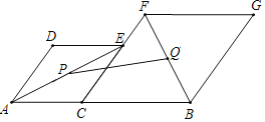
【题目】如图,已知AB=2![]() ,C为线段AB上的一个动点,分别以AC,CB为边在AB的同侧作菱形ACED和菱形CBGF,点C,E,F在一条直线上,∠D=120°.P、Q分别是对角线AE,BF的中点,当点C在线段AB上移动时,点P,Q之间的距离最短为_____(结果保留根号).
,C为线段AB上的一个动点,分别以AC,CB为边在AB的同侧作菱形ACED和菱形CBGF,点C,E,F在一条直线上,∠D=120°.P、Q分别是对角线AE,BF的中点,当点C在线段AB上移动时,点P,Q之间的距离最短为_____(结果保留根号).
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣ax+b的图象与反比例函数![]() 的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
的图象相交于点A(﹣4,﹣2),B(m,4),与y轴相交于点C.
(1)求反比例函数和一次函数的表达式;
(2)求点C的坐标及△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(-4,![]() ),B(-1,2)是一次函数y=kx+b的图像与反比例函数
),B(-1,2)是一次函数y=kx+b的图像与反比例函数![]() (m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
(m≠0,m<0)的函数图像的两个交点,AC⊥x轴于点C,BD⊥y轴于点D
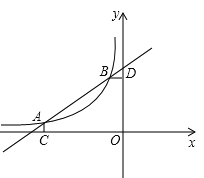
(1)根据函数图像直接回答问题:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
(2)求一次函数的表达式及m的值;
(3)点P是线段AB上一点,连接PC,PD,若△PCA和△PBD的面积相等,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
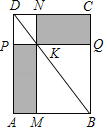
【题目】如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1_____S2;(填“>”或“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区的6名志愿者,在“十一”假期组织区内的未成年学生到公园秋游,公园的门票为每人40元,现有两种优惠方案,甲方案:志愿者免费,未成年学生按8折收费;乙方案:志愿者和未成年学生都按7折收费,若有![]() 名未成年学生.
名未成年学生.
(1)当![]() 时,甲方案需 元;乙方案需 元;
时,甲方案需 元;乙方案需 元;
(2)用含![]() 的式子表示两种方案各需多少元?
的式子表示两种方案各需多少元?
(3)当![]() 为何值时,甲、乙两种方案是一样的.
为何值时,甲、乙两种方案是一样的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点![]() 在数轴上分别对应的数为
在数轴上分别对应的数为![]() ,则
,则![]() 两点间的距离表示为
两点间的距离表示为![]() .
.
![]()
根据以上知识解题:
(1)若数轴上两点![]() 表示的数分别为
表示的数分别为![]() ,
,
①当![]() 时,
时,![]() 之间的距离为 ;
之间的距离为 ;
②![]() 之间的距离可用含
之间的距离可用含![]() 的式子表示为
的式子表示为![]() ;
;
③若该两点之间的距离为2,那么![]() 值为 .
值为 .
(2)![]() 的最小值为 ,此时
的最小值为 ,此时![]() 的取值范围是 ;
的取值范围是 ;
(3)若![]() ,则
,则![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别标有数字2,3,4的三张形状、大小一样的卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张卡片,求抽到奇数的概率;
(2)随机地抽取一张卡片,将卡片上标有的数字作为十位上的数字(不放回),再随机地抽取一张卡片,将卡片上标有的数字作为个位上的数字,组成的两位数恰好是“23”的概率是多少?
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com