Question

【题目】如图,CB∥OA,∠B=∠A=100°,E,F在CB上,且满足∠FOC=∠AOC,OE平分∠BOF.

(1)求∠EOC的度数.

(2)若平行移动AC,那么∠OCB∶∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.

Answer 1

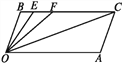
【答案】(1) 40°;(2) 不变, ∠OCB∶∠OFB=1∶2,理由见解析

【解析】（1）由于BC∥OA，∠B=100°，易求∠AOB，而OE、OC都是角平分线，从而可求∠COE；
（2）利用BC∥OA，可知∠AOC=∠BCO，又因为∠AOC=∠COF，所以就有∠FCO=∠FOC，即∠BFO=2∠FCO=2∠OCB，那么∠OCB：∠OFB=1：2；
解：(1)∵CB∥OA，

∴∠BOA+∠B=180°，

∴∠BOA=80°，

∵∠FOC=∠AOC，OE平分∠BOF，

∴∠EOC=∠EOF+∠FOC=∠BOF+∠FOA= (∠BOF+∠FOA)= ×80°=40°；

(2)不变。

∵CB∥OA，

∴∠OCB=∠COA，∠OFB=∠FOA，

∵∠FOC=∠AOC，

∴∠COA=∠FOA，即∠OCB:∠OFB=1:2.