
【题目】(1)如图![]() ,点
,点![]() 、
、![]() 分别在正方形
分别在正方形![]() 的边
的边![]() 、
、![]() 上,
上,![]() ,
,![]() ,
,![]() ,连结
,连结![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,使
,使![]() 与
与![]() 重合.求
重合.求![]() 的面积.
的面积.
(2)如图![]() ,四边形
,四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上,且
边上,且![]() ,求证:
,求证:![]() .
.


【答案】(1)15;(2)见解析
【解析】
(1)首先由旋转的性质,得出∠BAE=∠DAG,然后通过等角转换得出∠GAF=∠EAF =45°,根据SAS判定△AEF≌△AGF,两个三角形面积相等,即可得解;
(2)首先延长CB至G,使得BG=FD,连接AG,然后由![]() 得出∠GBA=∠FDA,再由BG=DF,
得出∠GBA=∠FDA,再由BG=DF,![]() 可判定△ABG≌△ADF,进而得出∠BAG=∠DAF,AG=AF,又由
可判定△ABG≌△ADF,进而得出∠BAG=∠DAF,AG=AF,又由![]() 得出∠EAG=∠EAF,加上AE=AE,可判定△AGE≌△AFE,得出GE=EF,即可得证.
得出∠EAG=∠EAF,加上AE=AE,可判定△AGE≌△AFE,得出GE=EF,即可得证.
(1)由已知得,∠BAE=∠DAG
∵∠BAE+∠EAD=90°
∴∠DAG+∠EAD=90°
又∵∠EAF=45°
∴∠GAF=∠EAF =45°
又∵AE=AG,AF=AF
∴△AEF≌△AGF(SAS)
∴EF=GF=5
∴![]()
(2)延长CB至G,使得BG=FD,连接AG,如图所示
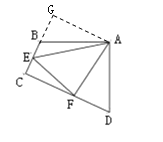
∵![]()
∴∠GBA=∠FDA
又∵BG=DF,![]()
∴△ABG≌△ADF(SAS)
∴∠BAG=∠DAF,AG=AF
又∵![]()
∴∠DAF+∠EAB=∠EAF
∴∠BAG+∠EAB=∠EAF
∴∠EAG=∠EAF
又∵AE=AE
∴△AGE≌△AFE(SAS)
∴GE=EF
∴BE+BG=EF
∴![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】901班的全体同学根据自己的兴趣爱好参加了六个学生社团(每个学生必须参加且只参加一个),为了了解学生参加社团的情况,学生会对该班参加各个社团的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“读书社”的学生有15人,请解答下列问题:

(1)该班的学生共有 名;
(2)若该班参加“吉他社”与“街舞社”的人数相同,请你计算,“吉他社”对应扇形的圆心角的度数;
(3)901班学生甲、乙、丙是“爱心社”的优秀社员,现要从这三名学生中随机选两名学生参加“社区义工”活动,请你用画树状图或列表的方法求出恰好选中甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一架梯子AB斜靠在墙面上,且AB的长为2.5米.

(1)若梯子底端离墙角的距离OB为0.7米,求这个梯子的顶端A距地面有多高?
(2)在(1)的条件下,如果梯子的顶端A下滑0.4米到点A′,那么梯子的底端B在水平方向滑动的距离BB′为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角板按图①所示的位置放置,图②是由它抽象画出的几何图形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() .
.
(1)请找出图②中与![]() 全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于非零实数a、b,规定ab=![]() ,若(x﹣3)(3﹣2x)=0,则x的值为_____;若关于x的方程(x﹣3)(3﹣2x)﹣(3﹣x)(mx﹣2)=﹣1无解,则m的值为_____.
,若(x﹣3)(3﹣2x)=0,则x的值为_____;若关于x的方程(x﹣3)(3﹣2x)﹣(3﹣x)(mx﹣2)=﹣1无解,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
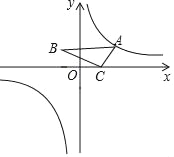
【题目】如图,O为坐标原点,点C的坐标为(1,0),∠ACB=90°,∠B=30°,当点A在反比例函数y=![]() 的图象上运动时,点B在函数_____(填函数解析式)的图象上运动.
的图象上运动时,点B在函数_____(填函数解析式)的图象上运动.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com