
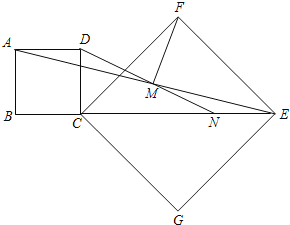
【题目】如图,正方形CGEF的对角线CE在正方形ABCD的边BC的延长线上(CG>BC),M是线段AE的中点,DM的延长线交CE于N.
(1)求证:AD=NE
(2)求证:①DM=MF;②DM⊥MF.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题
(1)由已知条件证:△ADM≌△ENM可得AD=NE;
(2)连接FD、FN,结合(1)中所得结论和已知条件可证△CDF≌△ENF,从而可得:FD=FN,∠3=∠4,由此可得:∠3+∠CFN=∠4+∠CFN=∠CFE=90°,这样可证得:△DFN是等腰直角三角形;再由△ADM≌△ENM可得DM=NM,就可得到:FM是等腰直角△DFN斜边上的中线,就可得到;DM=MF,DM⊥MF.
试题解析:
(1)∵四边形ABCD是正方形,
∴AD∥BC,∠BCD=90°,AD=CD,
∴∠MAD=∠MEN,
又∵M是AE的中点,
∴AM=EM
在△ADM和△ENM中,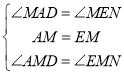 ,
,
∴△ADM≌△ENM(ASA),
∴AD=EN;
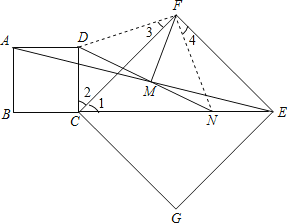
(2)连接FD、FN,
∵CE是正方形CGEF的对角线,
∴CF=EF,∠1=∠FEN=45°,
又∵∠BCD=90°,
∴∠DCE=90°,
∴∠2=∠1=∠FEN=45°,
在△CDF和△ENF中,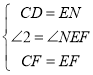 ,
,
∴△CDF≌△ENF(SAS)
∴∠3=∠4,DF=FN,
又∵∠CFN+∠4=90°,
∴∠CFN+∠3=90°,
∴△DFN是等腰直角三角形,
∵△ADM≌△ENM,
∴DM=NM,
∴FM=DM,FM⊥DM.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
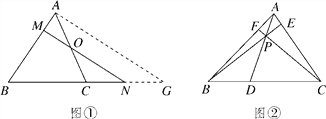
【题目】如图①所示,在△ABC中,点O是AC上一点,过点O的直线与AB,BC的延长线分别相交于点M,N.
【问题引入】
(1)若点O是AC的中点, ![]() ,求
,求![]() 的值;
的值;
温馨提示:过点A作MN的平行线交BN的延长线于点G.
【探索研究】
(2)若点O是AC上任意一点(不与A,C重合),求证: ![]() ;
;
【拓展应用】
(3)如图②所示,点P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F.若![]() ,
, ![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线![]() 与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在![]() 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于O点,BE平分∠ABO交AO于E点,CF⊥BE于F点,交BO于G点,连结EG、OF.则∠OFG的度数是( )
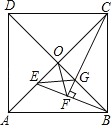
A.60°B.45°C.30°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若设计一种游戏方案:若从中任取一球(不放回),再从中任取一球。两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?请用画树状图或列表格的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受地震的影响,某超市鸡蛋供应紧张,需每天从外地调运鸡蛋1200斤.超市决定从甲、乙两大型养殖场调运鸡蛋,已知甲养殖场每天最多可调出800斤,乙养殖场每天最多可调出900斤,从两养殖场调运鸡蛋到超市的路程和运费如表:
到超市的路程(千米) | 运费(元/斤千米) | |
甲养殖场 | 200 | 0.012 |
乙养殖场 | 140 | 0.015 |
(1)若某天调运鸡蛋的总运费为2670元,则从甲、乙两养殖场各调运了多少斤鸡蛋?
(2)设从甲养殖场调运鸡蛋x斤,总运费为W元,试写出W与x的函数关系式,怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com