
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c=0无实数根;③a-b+c≥0;④![]() 的最小值为3,其中正确结论的个数是___________.
的最小值为3,其中正确结论的个数是___________.
【答案】3
【解析】
从抛物线与x轴最多一个交点及b>a>0,可以推断抛物线最小值最小为0,对称轴在y轴左侧,并得到b2-4ac≤0,从而得到①为正确,②错误;由x=-1及x=-2时y都大于或等于零可以得到③④正确.
∵b>a>0
∴-![]() <0,所以①正确;
<0,所以①正确;
∵抛物线与x轴最多有一个交点,
∴b2-4ac≤0,
∴关于x的方程ax2+bx+c=0有两个相等的实数根或无实数根;故②错误,
∵a>0及抛物线与x轴最多有一个交点,
∴x取任何值时,y≥0
∴当x=-1时,a-b+c≥0;所以③正确;
当x=-2时,4a-2b+c≥0,
a+b+c≥3b-3a,
a+b+c≥3(b-a),![]() ≥3,所以④正确.
≥3,所以④正确.
故答案为3个.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的的顶点为
的的顶点为![]() .
.
(1)顶点![]() 的坐标为 .
的坐标为 .
(2)横、纵坐标都是整数的点叫做整点.若![]()
![]() 轴且
轴且![]()
①点![]() 的坐标为 ;
的坐标为 ;
②过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,若直线
,若直线![]() 与抛物线交于
与抛物线交于![]() 两点,该抛物线在
两点,该抛物线在![]() 之间的部分与线段
之间的部分与线段![]() 所围成的区域(包括边界)恰有七个整点,结合函数图象,求
所围成的区域(包括边界)恰有七个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC的高AD四等分,过每一个分点作底边的平行线,把三角形的面积分成四部分S1、S2、S3、S4,则S1:S2:S3:S4等于( )
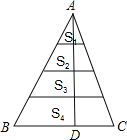
A.1:2:3:4B.2:3:4:5C.1:3:5:7D.3:5:7:9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以2cm/s的速度向点A匀速运动,同时动点N从点C出发,在CB边上以![]() cm/s的速度向点B匀速运动,设运动时间为ts(0≤t≤5),连接MN.
cm/s的速度向点B匀速运动,设运动时间为ts(0≤t≤5),连接MN.

发现:BM= cm,BN= cm;(用含t的式子来表示)
猜想:(1)若BM=BN,求t值;
(2)若△MBN与△ABC相似,求t值.
探究:是否存在符合条件的t,使△BMN与四边形AMNC面积相等?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD//BC,AD=2,AB=5,BC=10,点E是边BC上的一个动点(不与B,C重合),作∠AEF=∠AEB,使边EF交边CD于点F,(不与C,D重合),线段BE=______________时,△ABE与△CEF相似。
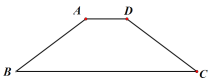
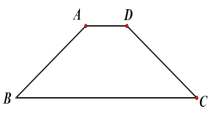
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这是水面宽度为10m。

(1)在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂用![]() 天时间生产一款新型节能产品,每天生产的该产品被某网店以每件
天时间生产一款新型节能产品,每天生产的该产品被某网店以每件![]() 元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第
元的价格全部订购,在生产过程中,由于技术的不断更新,该产品第![]() 天的生产成本
天的生产成本![]() (元/件)与
(元/件)与![]() (天)之间的关系如图所示,第
(天)之间的关系如图所示,第![]() 天该产品的生产量
天该产品的生产量![]() (件)与
(件)与![]() (天)满足关系式
(天)满足关系式![]()
![]() 第
第![]() 天,该厂生产该产品的利润是 元;
天,该厂生产该产品的利润是 元;
![]() 设第
设第![]() 天该厂生产该产品的利润为
天该厂生产该产品的利润为![]() 元.
元.
①求![]() 与
与![]() 之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
之间的函数关系式,并指出第几天的利润最大,最大利润是多少?
②在生产该产品的过程中,当天利润不低于![]() 元的共有多少天?
元的共有多少天?

查看答案和解析>>
科目:初中数学 来源: 题型:
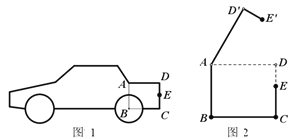
【题目】如图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D'到BC的距离;
(2)求E、E'两点的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com