Question

6．如图，P是△ABC的重心，过点P作PE∥AB交BC于点E，PF∥AC交BC于点F，若△PEF的周长是6，则△ABC的周长为18．

Answer 1

分析 延长AP交BC于Q，如图，根据三角形重心性质得$\frac{QP}{QA}$=$\frac{1}{3}$，再证明△QPE∽△QAB得到$\frac{PE}{AB}$=$\frac{QE}{QB}$=$\frac{QP}{QA}$=$\frac{1}{3}$，即AB=3PE，QB=3EQ，同理可得AC=3PF，GC=3QF，然后可得△ABC的周长=AB+AC+BC=3（PE+PF+EF）=18．

解答 解：延长AP交BC于Q，如图，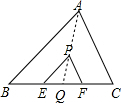
∵P是△ABC的重心，
∴$\frac{AP}{PQ}$=2，
∴$\frac{QP}{QA}$=$\frac{1}{3}$，
∵PE∥AB，
∴△QPE∽△QAB，
∴$\frac{PE}{AB}$=$\frac{QE}{QB}$=$\frac{QP}{QA}$=$\frac{1}{3}$，
∴AB=3PE，QB=3EQ，
同理可得AC=3PF，GC=3QF，
∴△ABC的周长=AB+AC+BC=3PE+3PF+3EF=3（PE+PF+EF）=3×6=18．
故答案为18．

点评 本题考查了三角形的重心：三角形的重心是三角形三边中线的交点；重心到顶点的距离与重心到对边中点的距离之比为2：1．也考查了相似三角形的判定与性质．