
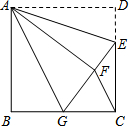
 如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 先计算出DE=2,EC=4,再根据折叠的性质AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,然后根据“HL”可证明Rt△ABG≌Rt△AFG,则GB=GF,∠BAG=∠FAG,所以∠GAE=$\frac{1}{2}$∠BAD=45°;GE=GF+EF=BG+DE;设BG=x,则GF=x,CG=BC-BG=6-x,在Rt△CGE中,根据勾股定理得(6-x)2+42=(x+2)2,解得x=3,则BG=CG=3,则点G为BC的中点;同时得到GF=GC,根据等腰三角形的性质得∠GFC=∠GCF,再由Rt△ABG≌Rt△AFG得到∠AGB=∠AGF,然后根据三角形外角性质得∠BGF=∠GFC+∠GCF,易得∠AGB=∠GCF,根据平行线的判定方法得到CF∥AG;过F作FH⊥DC,则△EFH∽△EGC,△EFH∽△EGC,由相似比为$\frac{2}{5}$,可计算S△FGC.
解答 解:∵正方形ABCD的边长为6,CE=2DE,
∴DE=2,EC=4,
∵把△ADE沿AE折叠使△ADE落在△AFE的位置,
∴AF=AD=6,EF=ED=2,∠AFE=∠D=90°,∠FAE=∠DAE,
在Rt△ABG和Rt△AFG中
$\left\{\begin{array}{l}{AB=AF}\\{AG=AG}\end{array}\right.$,
∴Rt△ABG≌Rt△AFG(HL),
∴GB=GF,∠BAG=∠FAG,
∴∠GAE=∠FAE+∠FAG=$\frac{1}{2}$∠BAD=45°,所以①正确;
设BG=x,则GF=x,C=BC-BG=6-x,
在Rt△CGE中,GE=x+2,EC=4,CG=6-x,
∵CG2+CE2=GE2,
∴(6-x)2+42=(x+2)2,解得x=3,
∴BG=3,CG=6-3=3
∴BG=CG,所以②正确;
∵EF=ED,GB=GF,
∴GE=GF+EF=BG+DE,所以③正确;
∵GF=GC,
∴∠GFC=∠GCF,
又∵Rt△ABG≌Rt△AFG,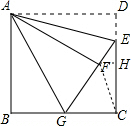
∴∠AGB=∠AGF,
而∠BGF=∠GFC+∠GCF,
∴∠AGB+∠AGF=∠GFC+∠GCF,
∴∠AGB=∠GCF,
∴CF∥AG,所以④正确;
过F作FH⊥DC
∵BC⊥DH,
∴FH∥GC,
∴△EFH∽△EGC,
∴$\frac{EH}{GC}=\frac{EF}{EG}$,
EF=DE=2,GF=3,
∴EG=5,
∴△EFH∽△EGC,
∴相似比为:$\frac{EH}{GC}=\frac{EF}{EG}$=$\frac{2}{5}$,
∴S△FGC=S△GCE-S△FEC=$\frac{1}{2}$×3×4-$\frac{1}{2}$×4×( $\frac{2}{5}$×3)=$\frac{18}{5}$=3.6,所以⑤正确.
故正确的有①②③④⑤,
故选:D.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了三角形全等的判定与性质、勾股定理和正方形的性质.


科目:初中数学 来源: 题型:选择题
| A. | |-6|=6 | B. | $(\frac{1}{2})^{-1}=-2$ | C. | $\sqrt{16}=±4$ | D. | a2•a3=a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.
为了解某学校学生一年中的课外阅读量,该校对800名学生采用随机抽样的方式进行了问卷调查,调查的结果分为四种情况:A、10本以下;B、10~15本;C、16~20本;D、20本以上.根据调查结果统计整理并制作了如图所示的两幅统计图表.| 各种情况人数统计频数分布表 | ||||
| 课外阅读情况 | A | B | C | D |
| 频数 | 20 | x | y | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
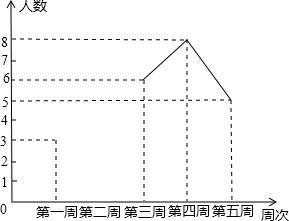 为配合我校开展的“书香校园”活动,校团委对我校某班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:
为配合我校开展的“书香校园”活动,校团委对我校某班同学近五周的读书情况进行了调查,将当周每日都坚持课外阅读的同学评为“读书之星”并将“读书之星”的人数与周次制成了如下不完整的折线统计图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com