
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊЕуBЃЈ0ЃЌ9ЃЉЃЌЕуCЮЊxжсЩЯвЛЖЏЕуЃЌСЌНгBCЃЌЁїODCКЭЁїEBCЖМЪЧЕШБпШ§НЧаЮЃЎ

ЃЈ1ЃЉЧѓжЄЃКDEЃНBOЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуDЧЁКУТфдкBCЩЯЪБЃЎ
ЂйЧѓЕуEЕФзјБъЃЛ
ЂкдкxжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁїPECЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЛ
ЂлШчЭМ3ЃЌЕуMЪЧЯпЖЮBCЩЯЕФЖЏЕуЃЈЕуBЃЌЕуCГ§ЭтЃЉЃЌЙ§ЕуMзїMGЁЭBEгкЕуGЃЌMHЁЭCEгкЕуHЃЌЕБЕуMдЫЖЏЪБЃЌMHЃЋMGЕФжЕЪЧЗёЗЂЩњБфЛЏЃПШєВЛЛсБфЛЏЃЌжБНгаДГіMHЃЋMGЕФжЕЃЛШєЛсБфЛЏЃЌМђвЊЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЂйEЃЈ6![]() ЃЌ9ЃЉЃЛЂкДцдкЃЌЕуPЕФзјБъЮЊЃЈЃ3
ЃЌ9ЃЉЃЛЂкДцдкЃЌЕуPЕФзјБъЮЊЃЈЃ3![]() ЃЌ0ЃЉЛђЃЈ9
ЃЌ0ЃЉЛђЃЈ9![]() ЃЌ0ЃЉЃЛЂлВЛБфЛЏЃЌMHЃЋMGЃН9
ЃЌ0ЃЉЃЛЂлВЛБфЛЏЃЌMHЃЋMGЃН9
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕШБпШ§НЧаЮЕФаджЪЕУЕНBC=CEЃЌOC=CDЃЌЁЯOCD=ЁЯBCE=60ЁуЃЌЧѓЕУЁЯOCB=ЁЯDCEЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉЂйгЩЕуBЃЈ0ЃЌ9ЃЉЃЌЕУЕНOB=9ЃЌИљОнШЋЕШШ§НЧаЮЕФаджЪЕУЕНЁЯCDE=ЁЯBOC=90ЁуЃЌИљОнЕШБпШ§НЧаЮЕФаджЪЕУЕНЁЯDEC=30ЁуЃЌЧѓЕУ![]() ЃЌЙ§EзїEFЁЭxжсгкFЃЌНЧШ§НЧаЮМДПЩЕУЕННсТлЃЛ
ЃЌЙ§EзїEFЁЭxжсгкFЃЌНЧШ§НЧаЮМДПЩЕУЕННсТлЃЛ
ЂкДцдкЃЌШчЭМЃЌЕБ![]() ЪБЃЌЕБCE=PEЃЌИљОнЕШбќШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЛЂлВЛЛсБфЛЏЃЌСЌНгEMЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЕУЕННсТлЃЎ
ЪБЃЌЕБCE=PEЃЌИљОнЕШбќШ§НЧаЮЕФаджЪМДПЩЕУЕННсТлЃЛЂлВЛЛсБфЛЏЃЌСЌНгEMЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНМДПЩЕУЕННсТлЃЎ
ЃЈ1ЃЉЁпЁїODCКЭЁїEBCЖМЪЧЕШБпШ§НЧаЮ
ЁрOCЃНDCЃЌBCЃНCEЃЌЁЯOCDЃНЁЯBCEЃН60Ёу
ЁрЁЯBCEЃЋЁЯBCDЃНЁЯOCDЃЋЁЯBCD
МДЁЯECDЃНЁЯBCO
ЁрЁїDECЁеЁїOBCЃЈSASЃЉ
ЁрDEЃНBO
ЃЈ2ЃЉЂйЁпЕуBЃЈ0ЃЌ9ЃЉЃЌ
ЁрOB=9ЃЌ
гЩЃЈ1ЃЉжЊЁїBCOЁеЁїECDЃЌ
ЁрЁЯCDE=ЁЯBOC=90ЁуЃЌ
ЁрDEЁЭBCЃЌ
ЁпЁїEBCЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯDEC=30ЁуЃЌ
ЁрЁЯOBC=ЁЯDEC=30ЁуЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Й§EзїEFЁЭxжсгкFЃЌ

ЁпЁЯDCO=ЁЯBCE=60ЁуЃЌ
ЁрЁЯECF=60ЁуЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрEЃЈ6![]() ЃЌ9ЃЉЃЛ
ЃЌ9ЃЉЃЛ
ЂкДцдкЃЌШчЭМЃЌ

ЕБ![]() ЪБЃЌ
ЪБЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЕБCE=PEЃЌ
ЁпЁЯECP=60ЁуЃЌ
ЁрЁїCPEЪЧЕШБпШ§НЧаЮЃЌ
ЁрP2ЃЌP3жиКЯЃЌ
ЁрЕБЁїPECЮЊЕШбќШ§НЧаЮЪБЃЌЕуPЕФзјБъЮЊЃЈЃ3![]() ЃЌ0ЃЉЛђЃЈ9
ЃЌ0ЃЉЛђЃЈ9![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЂлВЛЛсБфЛЏЃЌШчЭМЃЌСЌНгEMЃЌ
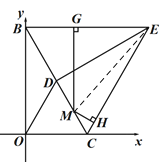
Ёп![]()
ЁпBC=CE=BEЃЌ
ЁрGM+MH=DE=9ЃЌ
ЁрMH+MGЕФжЕВЛЛсЗЂЩњБфЛЏЃЎ


 ПЮЪБбЕСЗНЫеШЫУёГіАцЩчЯЕСаД№АИ
ПЮЪБбЕСЗНЫеШЫУёГіАцЩчЯЕСаД№АИ ЛЦИдОЕфШЄЮЖПЮЬУЯЕСаД№АИ
ЛЦИдОЕфШЄЮЖПЮЬУЯЕСаД№АИ ЦєЖЋаЁЬтзївЕБОЯЕСаД№АИ
ЦєЖЋаЁЬтзївЕБОЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=mx+1ЕФЭМЯѓОЙ§ЕуAЃЈЉ1ЃЌ0ЃЉЃЌЧвгыЗДБШР§КЏЪ§![]() ЃЈkЁй0ЃЉНЛгкЕуBЃЈnЃЌ2ЃЉЃЎ
ЃЈkЁй0ЃЉНЛгкЕуBЃЈnЃЌ2ЃЉЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§ЕФНтЮіЪН
ЃЈ2ЃЉЧѓЗДБШР§КЏЪ§ЕФНтЮіЪН
ЃЈ3ЃЉжБНгаДГіЧѓЕБ1ЁмxЁм6ЪБЃЌЗДБШР§КЏЪ§yЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAFЁЮCDЃЌCBЦНЗжЁЯACDЃЌBDЦНЗжЁЯEBFЃЌЧвBCЁЭBDЃЌЯТСаНсТлЃКЂй BCЦНЗжЁЯABEЃЛЂк ACЁЮBEЃЛЂл ЁЯCBE+ЁЯDЃН90ЁуЃЛЂм ЁЯDEBЃН2ЁЯABCЃЎЦфжае§ШЗНсТлЕФИіЪ§гаЃЈЁЁЁЁЃЉ

A.1ИіB.2ИіC.3ИіD.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=Љ2x2+4x+6
ЃЈ1ЃЉЧѓКЏЪ§ЭМЯѓЕФЖЅЕуPзјБъМАЖдГЦжс
ЃЈ2ЃЉЧѓДЫХзЮяЯпгыxжсЕФНЛЕуAЁЂBзјБъ
ЃЈ3ЃЉЧѓЁїABPЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁїABCЕФЖЅЕузјБъЗжБ№ЮЊAЃЈЉ3ЃЌ2ЃЉЃЌBЃЈЉ4ЃЌ1ЃЉЃЌCЃЈЉ2ЃЌ0ЃЉЃЎ

ЃЈ1ЃЉШєНЋЁїABCЯђгвЦНвЦ3ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЧыЛГіЦНвЦКѓЕФЁїA1B1C1ЃЛ
ЃЈ2ЃЉШєЁїA2B2C2гыЁїABCЪЧжааФЖдГЦЭМаЮЃЌдђЖдГЦжааФЕФзјБъЮЊЁЁЁЁЁЁЁЁЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЙигкxЕФвЛДЮКЏЪ§y=(2m-1)x+m -2ЃЌШєЫќЕФКЏЪ§жЕyЫцxЕФдіДѓЖјдіДѓЃЌЧвЭМЯѓгыyжсИКАыжсЯрНЛЃЌЧвmЮЊе§ећЪ§ЃЎ
ЃЈ1ЃЉЧѓетИіКЏЪ§ЕФНтЮіЪНЃЎ
ЃЈ2ЃЉЧѓжБЯпy=ЃxКЭЃЈ1ЃЉжаКЏЪ§ЕФЭМЯѓгыxжсЮЇГЩЕФШ§НЧаЮУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЗДБШР§КЏЪ§![]() ЕФЭМЯѓЕФвЛжЇЮЛгкЕквЛЯѓЯоЃЎ
ЕФЭМЯѓЕФвЛжЇЮЛгкЕквЛЯѓЯоЃЎ
ЃЈ1ЃЉХаЖЯИУКЏЪ§ЭМЯѓЕФСэвЛжЇЫљдкЕФЯѓЯоЃЌВЂЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШчЭМЃЌOЮЊзјБъдЕуЃЌЕуAдкИУЗДБШР§КЏЪ§ЮЛгкЕквЛЯѓЯоЕФЭМЯѓЩЯЃЌЕуBгыЕуAЙигк![]() жсЖдГЦЃЌШєЁїOABЕФУцЛ§ЮЊ6ЃЌЧѓmЕФжЕЃЎ
жсЖдГЦЃЌШєЁїOABЕФУцЛ§ЮЊ6ЃЌЧѓmЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=-x2+ax+bЕФЭМЯѓгыxжсНЛгкAЃЈ-![]() ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌЧвгыyжсНЛгкЕуCЃЎ
ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌЧвгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЌВЂХаЖЯЁїABCЕФаЮзДЃЛ
ЃЈ2ЃЉЩшPЪЧxжсЩЯЗНЕФХзЮяЯпЩЯЕФЖЏЕуЃЌЙ§ЕуPзїPMЁЭxжсЃЌДЙзуЮЊMЃЌЪЧЗёДцдкЕуPЃЌЪЙЕУвдPЁЂA ЁЂMЮЊЖЅЕуЕФШ§НЧаЮгыABCЯрЫЦЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаУёгЊОМУГжајЗЂеЙЃЌ2017ФъГЧеђУёгЊЦѓвЕОЭвЕШЫЪ§ЭЛЦЦ20ЭђЃЎЮЊСЫНтГЧеђУёгЊЦѓвЕдБЙЄУПдТЕФЪеШызДПіЃЌЭГМЦОжЖдШЋЪаГЧеђУёгЊЦѓвЕдБЙЄ2017ФъдТЦНОљЪеШыЫцЛњГщбљЕїВщЃЌНЋГщбљЕФЪ§ОнАДЁА2000дЊвдФкЁБЁЂЁА2000дЊЁЋ4000дЊЁБЁЂЁА4000дЊЁЋ6000дЊЁБКЭЁА6000дЊвдЩЯЁБЗжЮЊЫФзщЃЌНјааећРэЃЌЗжБ№гУAЃЌBЃЌCЃЌDБэЪОЃЌЕУЕНЯТСаСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
гЩЭМжаЫљИјГіЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮГщбљЕїВщЕФдБЙЄга .ШЫЃЌдкЩШаЮЭГМЦЭМжаx ЕФжЕЮЊ .ЃЌБэЪОЁАдТЦНОљЪеШыдк2000дЊвдФкЁБЕФВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЪЧ .ЃЛ
ЃЈ2ЃЉНЋВЛЭъећЕФЬѕаЮЭМВЙГфЭъећЃЌВЂЙРМЦИУЪа2017ФъГЧеђУёгЊЦѓвЕ20ЭђдБЙЄжаЃЌУПдТЕФЪеШыдкЁА2000дЊЁЋ4000дЊЁБЕФдМЖрЩйШЫЃП

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com