
【题目】如图,某渔船向正东方向以12海里/时的速度航行,在A处测得岛C在北偏东的60°方向,1小时后渔船航行到B处,测得岛C在北偏东的30°方向,已知该岛周围10海里内有暗礁.
(1)B处离岛C有多远?
(2)如果渔船继续向东航行,有无触礁危险?

【答案】(1)B处离岛C有12海里;(2)没有触礁危险.
【解析】
(1) 过C作CO垂直AB,,通过证明∠ACB=∠CAB=30,即可求出CB的长;
(2)求出点C到AB的距离是否大于10,如果大于10则无触礁危险,反之则有.
(1)过C作CO垂直AB,
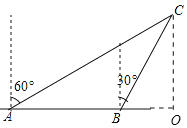
CO为渔船向东航行到C道最短距离
∵在A处测得岛C在北偏东的60°
∴∠CAB=30°
又∵B处测得岛C在北偏东30°,
∴∠CBO=60°,∠ABC=120°,
∴∠ACB=∠CAB=30°,
∴AB=BC=12×1=12(海里)(等边对等角);
(2)∵CO⊥AB,∠CBO=60°
∴CO=6![]() (海里)>10(海里)
(海里)>10(海里)
故如果渔船继续向东航行,没有触礁危险


 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】Rt△ABC中,AB=AC,D点为Rt△ABC外一点,且BD⊥CD,DF为∠BDA的平分线,当∠ACD=15°,下列结论:①∠ADC=45°;②AD=AF;③AD+AF=BD;④BC﹣CE=2D,其中正确的是( )

A.①③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
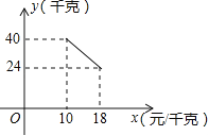
【题目】某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
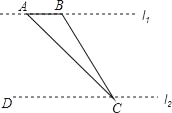
【题目】如图,为了测量河对岸l1上两棵古树A、B之间的距离,某数学兴趣小组在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则A、B之间的距离为( )
A. 50m B. 25m C. (50﹣![]() )m D. (50﹣25
)m D. (50﹣25![]() )m
)m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,线段AM为BC边上的中线.动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,连结BE.
(1)求∠CAM的度数;
(2)若点D在线段AM上时,求证:△ADC≌△BEC;
(3)当动D在直线AM上时,设直线BE与直线AM的交点为O,试判断∠AOB是否为定值?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,CD=BE,DG⊥BC于点 G,EF⊥BC于点 F,且 DG=EF.

(1)求证:△DGC≌△EFB.
(2)连结 BD,CE. 求证:BD=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
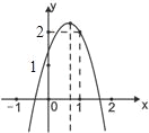
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中﹣1<x1<0.1<x2<2.下列结论:4a+2b+c<0;2a+b<0;b2+8a>4ac;
a<﹣1;其中结论正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E、F分别为PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2.若S=3,则S1+S2的值为( )

A. 3 B. 6 C. 12 D. 24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com