
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中点A到点B的距离为3,点C到点B的距离为7,如图所示:设点A,B,C所对应的数的和是m.
![]()
(1)若以C为原点,则m的值是_______;
(2)若原点0在图中数轴上,且点C到原点0的距离为4,求m的值;
(3)动点P从A点出发,以每秒2个单位长度的速度向终点C移动,动点Q同时从B点出发,以每秒1个单位的速度向终点C移动,当几秒后,P、Q两点间的距离为2?(直接写出答案即可)
【答案】(1)-17;(2)m=-5或-29;(3)当1秒或5秒后,P、Q两点间的距离为2.
【解析】
(1)根据已知点A到点B的距离为3和点C到点B的距离为7求出即可;
(2)分为两种情况,当O在C的左边时,当O在C的右边时,求出每种情况A、B、C对应的数,即可求出m;
(3)分为两种情况,当P在Q的左边时,当P在Q的左边时,假如C为原点,求出P、Q对应的数,列出算式,即可求出t.
(1)当以C为原点时,A、B对应的数分别为-7,-10,m=-10+(-7)+0=-17,
故答案为:7,-17;
(2)当O在C的左边时,A、B、C三点在数轴上所对应的数分别为-6、-3、4,
则m=-6-3+4=-5,
当O在C的右边时,A、B、C三点在数轴上所对应的数分别为-14、-11、-4,
则m=-14-11-4=-29,
综上所述:m=-5或-29;
(3)假如以C为原点,则A、B、C对应的数为-10,-7,0,Q对应的数是-(7-t),P对应的数是-(10-2t),
当P在Q的左边时,[-(7-t)]-[-(10-2t)]=2,
解得:t=1,
当P在Q的左边时,[-(10-2t)]-[-(7-t)]=2,
解得:t=5,
即当1秒或5秒后,P、Q两点间的距离为2.


科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寓言故事《乌鸦喝水》教导我们遇到困难要运用智慧、认真思考才能让问题迎刃而解.如图,一个紧口瓶中盛有一些水,可乌鸦的嘴够不到瓶中的水.于是乌鸦衔来一些小石子放入瓶中,瓶中的水面高度得到提升.由于放入的石子较多,水都快溢出来了,乌鸦成功喝到了水,如果衔入瓶中石子的体积为![]() ,水面高度为
,水面高度为![]() ,下面图象能大致表示该故事情节的是( )
,下面图象能大致表示该故事情节的是( )
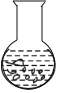
A.  B.
B. 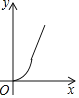 C.
C. 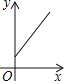 D.
D. 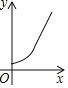
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年是我们伟大祖国建国70周年,各种欢庆用品在网上热销.某网店销售甲、乙两种纪念商品,甲种商品每件进价150元,可获利润40元;乙种商品每件进价100元,可获利润30元.由于这两种商品特别畅销,网店老板计划再购进两种商品共100件,其中乙种商品不超过36件.
(1)若购进这100件商品的费用不得超过13700元,求共有几种进货方案?
(2)在(1)的条件下,该网店在71建党节当天对甲种商品以每件优惠m(0<m<20)元的价格进行优惠促销活动,乙种商品价格不变,那么该网店应如何调整进货方案才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
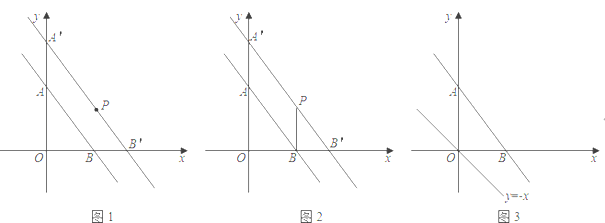
【题目】知识再现:
如果![]() ,
,![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为![]() ;对于两个一次函数
;对于两个一次函数![]() 和
和![]() ,若两个一次函数图象平行,则
,若两个一次函数图象平行,则![]() 且
且![]() ;若两个一次函数图象垂直,则
;若两个一次函数图象垂直,则![]() .
.
提醒:在下面这个相关问题中如果需要,你可以直接利用以上知识.
在平面直角坐标系中,已知点![]() ,
,![]() .
.
(1)如图1,把直线![]() 向右平移使它经过点
向右平移使它经过点![]() ,如果平移后的直线交
,如果平移后的直线交![]() 轴于点
轴于点![]() ,交x轴于点
,交x轴于点![]() ,请确定直线
,请确定直线![]() 的解析式.
的解析式.
(2)如图2,连接![]() ,求
,求![]() 的长.
的长.
(3)已知点![]() 是直线
是直线![]() 上一个动点,以
上一个动点,以![]() 为对角线的四边形
为对角线的四边形![]() 是平行四边形,当
是平行四边形,当![]() 取最小值时,请在图3中画出满足条件的
取最小值时,请在图3中画出满足条件的![]() ,并直接写出此时
,并直接写出此时![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市政府要求武汉轻轨二七路段工程12个月完工。现由甲、乙两工程队参与施工,已知甲队单独完成需要16个月,每月需费用600万元;乙队单独完成需要24个月,每月需费用400万元。由于前期工程路面较宽,可由甲、乙两队共同施工。随着工程的进行,路面变窄,两队再同时施工,对交通影响较大,为了减小对解放大道的交通秩序的影响,后期只能由一个工程队施工.工程总指挥部结合实际情况现拟定两套工程方案:
①先由甲、乙两个工程队合做m个月后,再由甲队单独施工,保证恰好按时完成.
②先由甲、乙两个工程队合做n个月后,再由乙队单独施工,也保证恰好按时完成.
⑴求两套方案中m和n的值;
⑵通过计算,并结合施工费用及施工对交通的影响,你认为该工程总指挥部应该选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
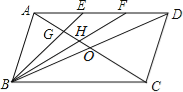
(1)求EG:BG的值;
(2)求证:AG=OG;
(3)设AG=a,GH=b,HO=c,求a:b:c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com