
【题目】知识再现:
如果![]() ,
,![]() ,则线段
,则线段![]() 的中点坐标为
的中点坐标为![]() ;对于两个一次函数
;对于两个一次函数![]() 和
和![]() ,若两个一次函数图象平行,则
,若两个一次函数图象平行,则![]() 且
且![]() ;若两个一次函数图象垂直,则
;若两个一次函数图象垂直,则![]() .
.
提醒:在下面这个相关问题中如果需要,你可以直接利用以上知识.
在平面直角坐标系中,已知点![]() ,
,![]() .
.
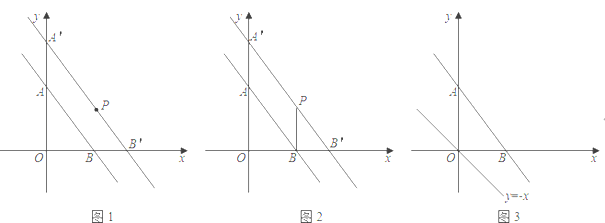
(1)如图1,把直线![]() 向右平移使它经过点
向右平移使它经过点![]() ,如果平移后的直线交
,如果平移后的直线交![]() 轴于点
轴于点![]() ,交x轴于点
,交x轴于点![]() ,请确定直线
,请确定直线![]() 的解析式.
的解析式.
(2)如图2,连接![]() ,求
,求![]() 的长.
的长.
(3)已知点![]() 是直线
是直线![]() 上一个动点,以
上一个动点,以![]() 为对角线的四边形
为对角线的四边形![]() 是平行四边形,当
是平行四边形,当![]() 取最小值时,请在图3中画出满足条件的
取最小值时,请在图3中画出满足条件的![]() ,并直接写出此时
,并直接写出此时![]() 点坐标.
点坐标.
【答案】(1)![]() ;(2)5;(3)
;(2)5;(3)![]()
【解析】
(1)用待定系数法可求直线AB的解析式,由平移的性质可设直线A'B'的解析式为:![]() ,将点P坐标代入可求直线A′B′的解析式;
,将点P坐标代入可求直线A′B′的解析式;
(2)由P(6,4),B(6,0),点B'坐标(9,0)可得BP⊥B'B,BP=4,BB'=3,由勾股定理可求B'P的长;
(3)由平行四边形的性质可得![]() ,AE=BE,当CE⊥CO时,CE的值最小,即CD的值最小,由中点坐标公式可求点E坐标,可求CE解析式,列出方程组可求点C坐标.
,AE=BE,当CE⊥CO时,CE的值最小,即CD的值最小,由中点坐标公式可求点E坐标,可求CE解析式,列出方程组可求点C坐标.
解:(1)设直线![]() 的解析式为:
的解析式为:![]() ,过点
,过点![]() 两点,有
两点,有
∴![]() ,∴
,∴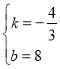
直线![]() 的解析式为:
的解析式为: ![]() ,
,
把直线![]() 向右平移使它经过点
向右平移使它经过点![]()
∴直线![]() 的解析式为
的解析式为![]() ,且过点
,且过点![]()
∴![]() ,∴
,∴![]()
∴直线![]() 的解析式为
的解析式为![]()
(2)∵直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]()
∴当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]()
∵![]() ,
,![]() ,点
,点![]() 坐标
坐标![]()
∴![]() 轴,
轴,![]() ,
,![]() ,
,
∴![]()
(3)如图,设![]() 与
与![]() 的交点为
的交点为![]() ,
,

∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴要使![]() 取最小值,即
取最小值,即![]() 的值最小,
的值最小,
由垂线段最短可得:当![]() 时,
时,![]() 的值最小,即
的值最小,即![]() 的值最小,
的值最小,
∵点![]() ,
,![]() ,且
,且![]()
∴点![]()
∵![]() ,直线
,直线![]() 解析式为:
解析式为:![]()
∴设![]() 解析式为
解析式为![]() ,且过点
,且过点![]()
∴![]()
∴![]()
∴![]() 解析式为
解析式为![]()
∴联立直线![]() 和
和![]() 的解析式成方程组,得
的解析式成方程组,得![]()
解得: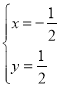
∴点![]()


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】某校七年级学生乘车去参加社会实践话动,若每辆客车乘50人,还有12人不能上车;若每辆客车乘55人,则最后一辆空了8个座位,求该校租了多少辆客车?七年级学生多少人?
根据题意,小明、小红分别列出了尚不完整的方程如下:
小明:50x口![]()
![]() 口
口![]()
![]() ;小红:
;小红:![]()
(其中“口”表示运算符号,“![]()
![]() ”表示数字)
”表示数字)
![]() 小明所列方程中x表示的意义是:______;小红所列方程中y表示的意义是:______;
小明所列方程中x表示的意义是:______;小红所列方程中y表示的意义是:______;
![]() 请你把小明或小红所列方程补充完整,并相应解答.
请你把小明或小红所列方程补充完整,并相应解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
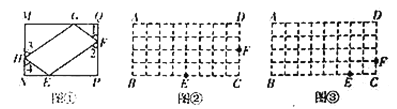
【题目】(问题原型)在图①的矩形![]() 中,点
中,点![]() 、
、![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 、
、![]() 上,若
上,若![]() ,则称四边形
,则称四边形![]() 为矩形
为矩形![]() 的反射四边形;
的反射四边形;
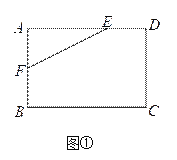
(操作与探索)在图②,图③的矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边的格点上,试利用正方形网格分别在图②、图③上作矩形
边的格点上,试利用正方形网格分别在图②、图③上作矩形![]() 的反射四边形
的反射四边形![]() ;
;
(发现与应用)由前面的操作可以发现,一个矩形有不同的反射四边形,且这些反射四边形的周长都相等.若在图①的矩形![]() 中,
中,![]() ,
,![]() ,则其反射四边形
,则其反射四边形![]() 的周长为______.
的周长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
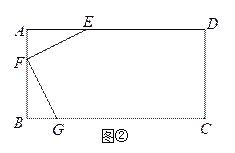
【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);
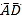
(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方法感悟:
(1)如图①,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决:
(2)如图②,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=![]() 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中点A到点B的距离为3,点C到点B的距离为7,如图所示:设点A,B,C所对应的数的和是m.
![]()
(1)若以C为原点,则m的值是_______;
(2)若原点0在图中数轴上,且点C到原点0的距离为4,求m的值;
(3)动点P从A点出发,以每秒2个单位长度的速度向终点C移动,动点Q同时从B点出发,以每秒1个单位的速度向终点C移动,当几秒后,P、Q两点间的距离为2?(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() 的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+
的图象如图所示,A,P为该图象上的点,且关于原点成中心对称.在△PAB中,PB∥y轴,AB∥x轴,PB与AB相交于点B.若△PAB的面积大于12,则关于x的方程(a-1)x2-x+![]() =0的根的情况是________________.
=0的根的情况是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,任意长为半径画弧,分别交AB,AC于点M和N,再分别以点M,N为圆心,大于![]() MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
MN长为半径画弧,两弧交于点P,连结AP并延长,交BC于点D,则下列说法中,正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC∶S△ABC=1∶3.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
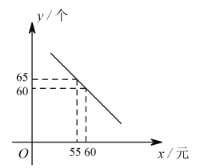
【题目】某体育用品商店试销一款成本为 50 元的排球,规定试销期间单价不低于成本价,且获利不得高于 40%。经试销发现,销售量 ![]() (个)与销售单价
(个)与销售单价 ![]() (元)之间满足如图所示的一次函数关系.
(元)之间满足如图所示的一次函数关系.
(1)试确定![]() 与
与 ![]() 之间的函数关系式;
之间的函数关系式;
(2)若该体育用品商店试销的这款排球所获得的利润为 ![]() 元,试写出利润
元,试写出利润 ![]() (元)与销售单价
(元)与销售单价 ![]() (元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
(元)之间的函数关系式;当试销单价定为多少元时,该商店可获最大利润?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com