
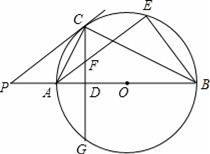
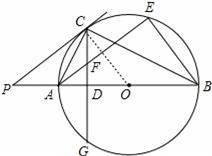
如图,AB为⊙O的直径,P是BA延长线一点,PC切⊙O于点C,CG是⊙O的弦,CG⊥AB,垂足为D.
(1)求证:△ACD∽△ABC;
(2)求证:∠PCA=∠ABC;
(3)过点A作AE∥PC交⊙O于点F,连接BE,若sin∠P=
 ,CF=5,求BE的长.
,CF=5,求BE的长.

【考点】圆的综合题.
【分析】(1)欲证明△ACD∽△ABC,只要证明①∠ADC=∠ACB,②∠CAD=∠BAC即可.
(2)利用等角的余角相等证明,即证明∠PCA+∠OCA=90°以及∠ABC+∠OAC=90°由此可以解决问题.
(3)先证明FA=FC=5,在RT△ADF中,根据sin∠FAD=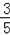
 求出DF、AD,在RT△COD中利用勾股定理求出半径,最后在RT△ABE中利用sin∠BAE=
求出DF、AD,在RT△COD中利用勾股定理求出半径,最后在RT△ABE中利用sin∠BAE=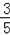
 求出BE即可.
求出BE即可.
【解答】(1)证明:∵AB是直径,
∴∠ACB=90°,
∵CG⊥AB,
∴∠ADC=90°=∠ACB,
∵∠CAD=∠BAC,
∴△ACD∽△ABC.
(2)证明:连接OC.
∵PC切⊙O于C,
∴OC⊥PC,
∴∠PCO=90°
∴∠PCA+∠OCA=90°,
∵∠ACB=90°,
∴∠ABC+∠OAC=90°,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠PCA=∠ABC.
(3)解:∵AE∥PC,
∴∠PCA=∠CAF,
∵AB⊥CG,
∴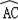
 =
=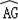
 ,
,
∴∠ACF=∠ABC,
∵∠PCA=∠BC,
∴∠ACF=∠CAF,
∴FA=FC,
∵CF=5,
∴AF=5,
∵AE∥PC,
∴∠FAD=∠P,
∵sin∠P=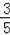
 ,
,
∴sin∠FAD=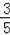
 ,
,
∴FD=3,AD=4,CD=8,
在RT△COD中,设CO=r,则有r2=(r﹣4)2+82
∴r=10,
∴AB=2r=20,
∵AB是直径,
∴∠AEB=90°,
∴sin∠EAB=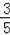
 ,
,
∴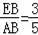
 ,
,
∴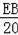
 =
=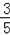
 ,
,
∴EB=12.

【点评】本题考查圆的有关知识、相似三角形的判定和性质、三角函数、勾股定理等知识,注意连接OC是圆中常用辅助线,熟练掌握垂径定理、切线的性质是解题的关键,属于中考压轴题.


科目:初中数学 来源: 题型:
如图所示,在边长为1的小正方形组成的网格中, 的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母。
的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母。
(1)作 ,使得
,使得 与
与 关于直线
关于直线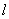 对称;
对称;
 (2)求
(2)求 的面积(直接写出结果)。
的面积(直接写出结果)。
查看答案和解析>>
科目:初中数学 来源: 题型:
以下说法正确的是( )
A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是

B.随机抛掷一枚均匀的硬币,落地后反面一定朝上
C.某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖
D.在一次课堂进行的抛硬币试验中,同学们估计硬币落地后正面朝上的概率为0.51
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中
(1)作图,作BC边的垂直平分线分别交于AC,BC于点D,E(用尺规作图法,保留作图痕迹,不要求写作法)
(2)在(1)条件下,连接BD,若BD=9,BC=12,求∠C的余弦值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com