
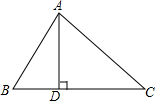
 如图,在△ABC中,AD是BC边上的高,∠B=45°,∠C=60°,AD=2,求BC的长.(结果保留根号)
如图,在△ABC中,AD是BC边上的高,∠B=45°,∠C=60°,AD=2,求BC的长.(结果保留根号) 分析 分别在RT△ABD和RT△ADC中根据勾股定理和等腰直角三角形的性质求得BD、CD的长,则BC=BD+DC,由此其值就可以得到了.
解答 解:∵AD是BC边上的高,∠C=60°,
∴∠CAD=30°,
∴CD=$\frac{1}{2}$AC,
在Rt△ACD中,根据勾股定理,
AC2-CD2=AD2,
(2CD)2-CD2=AD2,
∴CD=$\frac{{2\sqrt{3}}}{3}$,
∵AD是BC边上的高,∠B=45°,
∴∠BAD=45°,
∴BD=AD=2,
∴BC=BD+CD=$2+\frac{{2\sqrt{3}}}{3}$.
点评 此题考查了勾股定理,求一般三角形的边常用的方法就是作高,从而把一般三角形的问题转化到直角三角形中进行求解.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.
如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
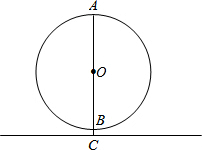 如图,⊙O是梦幻谷的摩天轮示意图,⊙O的最高处A到地面的距离是23米,最低处B到地面的距离是3米,AB是直径,摩天轮匀速转动,从B处乘坐绕摩天轮一周要6分钟,
如图,⊙O是梦幻谷的摩天轮示意图,⊙O的最高处A到地面的距离是23米,最低处B到地面的距离是3米,AB是直径,摩天轮匀速转动,从B处乘坐绕摩天轮一周要6分钟,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,两个等腰三角形的顶角互补,其中一个三角形的边长是a,a,b(a>b),另一个三角形的边长为b,b,a,则这两个三角形的六个内角中,度数最大的是( )
如图所示,两个等腰三角形的顶角互补,其中一个三角形的边长是a,a,b(a>b),另一个三角形的边长为b,b,a,则这两个三角形的六个内角中,度数最大的是( )| A. | 75° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com