
【题目】如图,在平面直角坐标系xOy中,已知点A(1,2),B(3,2),连接AB.若对于平面内一点P,线段AB上都存在点Q,使得PQ≤2,则称点P是线段AB的“影子”.
(1)在点C(0,1),D(2,![]() ),E(4,5)中,线段AB的”影子”是 .
),E(4,5)中,线段AB的”影子”是 .
(2)若点M(m,n)在直线y=-x+2上,且不是线段AB的“影子”,求m的取值范围.
(3)若直线y=![]() x+b上存在线段AB的“影子”,求b的取值范围以及“影子”构成的区域面积.
x+b上存在线段AB的“影子”,求b的取值范围以及“影子”构成的区域面积.
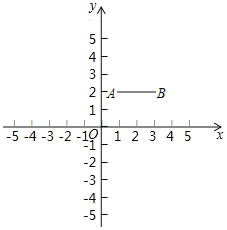
【答案】(1)C,D;(2)m<![]() 或m>2;;(3)4π+8.
或m>2;;(3)4π+8.
【解析】
(1)根据A、B的坐标得出AB∥x轴,根据点P到直线AB的距离≤2,求出当横坐标-1≤x≤3纵坐标2≤y≤4范围内时,点是线段AB的“临近点”,看点的纵坐标是否在y的范围内即可以及在A点的左边到A点的距离≤2,或在B点的右边到B点的距离≤2,点是线段AB的“临近点”;
(2)如图,设直线线y=-x+2交“影子”于点C,F,如图所示,延长BA交y轴于E,过C作CD⊥BA于BA的延长线于D,结合图形和一次函数图象上点的坐标特征来求m的范围;
(3)当直线y=![]() x+b与半圆A相切、与半圆B相切来求b的最值,从而得到b的取值范围.
x+b与半圆A相切、与半圆B相切来求b的最值,从而得到b的取值范围.
(1)C(0,1),D(2,![]() )是线段AB的“临近点”.理由是:
)是线段AB的“临近点”.理由是:
∵点P到直线AB的距离≤2,A、B的纵坐标都是2,
∴AB∥x轴,2-2=0,2+2=4,
∴当横坐标-1≤x≤3纵坐标2≤y≤4范围内时,该点是线段AB的“临近点”,
∵D(2,![]() ),
),
∴D(2,![]() )是线段AB的“临近点”;
)是线段AB的“临近点”;
∵C(0,1),A(1,2),
∴AC=1-0=1,
∴C(0,1)是线段AB的“临近点”.
故答案为:C和D;
(2)设直线线y=-x+2交“影子”于点C,F,如图所示,延长BA交y轴于E,过C作CD⊥BA于BA的延长线于D,
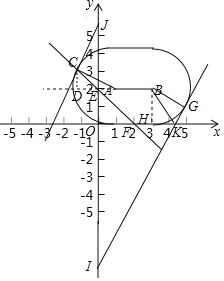
在Rt△ADC中,设D(x,2),则DE=-x,CD=-x,
∴DA=1-x,AC=2,
∴(-x)2+(1-x)2=4,
解得:x1=![]() ,x2=
,x2=![]() ,
,
∵直线y=-x+2与x轴的解得为F(2,0),
∴m<![]() 或m>2;
或m>2;
(3)设直线y=![]() x+b与半圆B相切于G,与x轴交于k,与y轴交于I,过B作BH⊥x轴于H,
x+b与半圆B相切于G,与x轴交于k,与y轴交于I,过B作BH⊥x轴于H,
则H(3,0),
在Rt△BHK中,BH=2,∠BKH=60°,
∴HK=![]() ,
,
在Rt△OKI中,OI=3![]() +2,则I(0,-3
+2,则I(0,-3![]() -2),
-2),
同理J(0,6-![]() ),
),
∴b的取值范围:-2-3![]() ≤b≤6-
≤b≤6-![]() ,
,
∵“影子”构成的区域为两个半圆和一个矩形,
∴影子”构成的区域面积=22π+4×2=4π+8.


科目:初中数学 来源: 题型:
【题目】一声汽笛长鸣,火车开进了蔡家崖.这是我省吕梁革命老区人民期盼已久的客运列车.蔡家崖列车的开通.带动老区驶入了发展红色旅游的快车进.某旅行社对去年“国庆”期间到吕梁观光的游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,回答下列问题:

(1)求本次抽样调查的总人数:
(2)补全条形统计图;
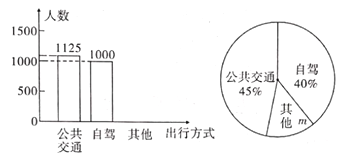
(3)扇形统计图中“其他”部分扇形的圆心角度数为____;
(4)去年“国庆”期问到吕梁观光的旅游者为275万人,则选择自驾方式出行的有多少万人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A1,A2,A3和B1,B2,B3分别在直线y=![]() 和x轴上,△OA1B1,△B1A2B2,△B2A3B3都是等腰直角三角形.则A3的坐标为_______.
和x轴上,△OA1B1,△B1A2B2,△B2A3B3都是等腰直角三角形.则A3的坐标为_______.
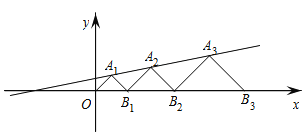 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
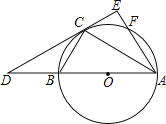
【题目】如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且点C是![]() 的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
(1)求证:AE⊥DE;
(2)若∠BAF=60°,AF=4,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
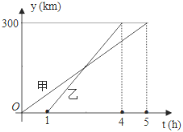
【题目】甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶时间x(小时)之间的函数关系如图所示,根据图象提供的信息,解决下列问题:
(1)A,B两城相距 千米;
(2)分别求甲、乙两车离开A城的距离y与x的关系式.
(3)求乙车出发后几小时追上甲车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船航行到 B 处时,测得小岛 A 在船的北偏东 60°的方向,轮船从 B 处继续向正东方向航行 20 海里到达 C 处时,测得小岛 A 在北船的北偏东 30°的方向.
(1)若小岛 A 到这艘轮船航行路线 BC 的距离是 AD,求 AD 的长.
(2)已知在小岛周围 17 海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?(![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
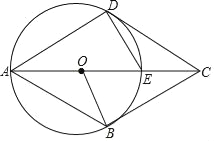
【题目】已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线;
(3)在(2)的条件下,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
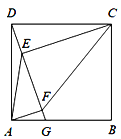
【题目】如图,在正方形ABCD中,点G在边AB上(不与点A,B重合),连接DG,作CE⊥DG于点E,AF⊥DG于点F,连接AE,CF.
(1)求证:DE=AF;
(2)若![]() 设
设![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com