
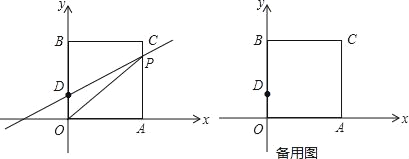
ЁОЬтФПЁПШчЭМдкЦНУцжБНЧзјБъЯЕжаЃЌOЪЧзјБъдЕуЃЌГЄЗНаЮOACBЕФЖЅЕуAЃЌBЗжБ№дкxЃЌyжсЩЯЃЌвбжЊOAЃН3ЃЌЕуDЮЊyжсЩЯвЛЕуЃЌЦфзјБъЮЊЃЈ0ЃЌ1ЃЉЃЌCDЃН5ЃЌЕуPДгЕуAГіЗЂвдУПУы1ИіЕЅЮЛЕФЫйЖШбиЯпЖЮAЉCЉBЕФЗНЯђдЫЖЏЃЌЕБЕуPгыЕуBжиКЯЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЮЊtУы
ЃЈ1ЃЉЧѓBЃЌCСНЕузјБъЃЛ
ЃЈ2ЃЉЂйЧѓЁїOPDЕФУцЛ§SЙигкtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЕБЕуDЙигкOPЕФЖдГЦЕуEТфдкxжсЩЯЪБЃЌЧѓЕуEЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЂкЧщПіЯТЃЌжБЯпOPЩЯЧѓвЛЕуFЃЌЪЙFE+FAзюаЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉBЃЈ0ЃЌ5ЃЉЃЌCЃЈ3ЃЌ5ЃЉЃЛЃЈ2ЃЉЂйSЃНЃ![]() ЃЛЂкEЃЈ1ЃЌ0ЃЉЃЛЃЈ3ЃЉADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдђЕуFМДЮЊЫљЧѓ
ЃЛЂкEЃЈ1ЃЌ0ЃЉЃЛЃЈ3ЃЉADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдђЕуFМДЮЊЫљЧѓ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЫФБпаЮOACBЪЧОиаЮЃЌЕУЕНBCЃНOAЃН3ЃЌдкRtЁїBCDжаЃЌгЩЙДЙЩЖЈРэЕУЕНBDЃН![]() ЃН4ЃЌOBЃН5ЃЌДгЖјЧѓЕУЕуЕФзјБъЃЛ
ЃН4ЃЌOBЃН5ЃЌДгЖјЧѓЕУЕуЕФзјБъЃЛ
ЃЈ2ЃЉЂйЕБЕуPдкACЩЯЪБЃЌODЃН1ЃЌBCЃН3ЃЌSЃН![]() ЃЌЕБЕудкBCЩЯЪБЃЌODЃН1ЃЌBPЃН5+3ЉtЃН8ЉtЃЌЕУЕНSЃН
ЃЌЕБЕудкBCЩЯЪБЃЌODЃН1ЃЌBPЃН5+3ЉtЃН8ЉtЃЌЕУЕНSЃН![]() ЁС1ЁСЃЈ8ЉtЃЉЃНЉ
ЁС1ЁСЃЈ8ЉtЃЉЃНЉ![]() t+4ЃЛ
t+4ЃЛ
ЂкЕБЕуDЙигкOPЕФЖдГЦЕуТфдкxжсЩЯЪБЃЌЕУЕНЕуDЕФЖдГЦЕуЪЧЃЈ1ЃЌ0ЃЉЃЌЧѓЕУEЃЈ1ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉгЩЕуDЁЂEЙигкOPЖдГЦЃЌСЌНгADНЛOPгкFЃЌевЕНЕуFЃЌДгЖјШЗЖЈADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдкRtЁїAODжаЃЌгЩЙДЙЩЖЈРэЧѓЕУADЃН![]() ЃЌМДAF+EFЕФзюаЁжЕЃН
ЃЌМДAF+EFЕФзюаЁжЕЃН![]() ЃЎ
ЃЎ
НтЃКЃЈ1ЃЉЁпЫФБпаЮOACBЪЧОиаЮЃЌ
ЁрBCЃНOAЃН3ЃЌ
дкRtЁїBCDжаЃЌЁпCDЃН5ЃЌBCЃН3ЃЌ
ЁрBDЃН![]() ЃН4ЃЌ
ЃН4ЃЌ
ЁрOBЃН5ЃЌ
ЁрBЃЈ0ЃЌ5ЃЉЃЌCЃЈ3ЃЌ5ЃЉЃЛ
ЃЈ2ЃЉЂйЕБЕуPдкACЩЯЪБЃЌODЃН1ЃЌBCЃН3ЃЌ
ЁрSЃН![]() ЃЌ
ЃЌ
ЕБЕудкBCЩЯЪБЃЌODЃН1ЃЌBPЃН5+3ЉtЃН8ЉtЃЌ
ЁрSЃН![]() ЁС1ЁСЃЈ8ЉtЃЉЃНЉ
ЁС1ЁСЃЈ8ЉtЃЉЃНЉ![]() t+4ЃЛЃЈtЁн0ЃЉ
t+4ЃЛЃЈtЁн0ЃЉ
ЂкЕБЕуDЙигкOPЕФЖдГЦЕуТфдкxжсЩЯЪБЃЌЕуDЕФЖдГЦЕуЪЧЃЈ1ЃЌ0ЃЉЃЌ
ЁрEЃЈ1ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉШчЭМ2ЁпЕуDЁЂEЙигкOPЖдГЦЃЌСЌНгADНЛOPгкFЃЌ
дђADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдђЕуFМДЮЊЫљЧѓЃЎ
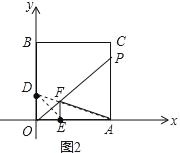
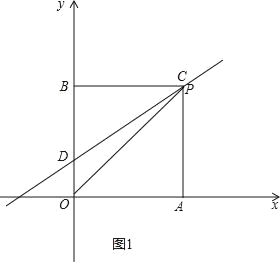
ЙЪД№АИЮЊЃКЃЈ1ЃЉBЃЈ0ЃЌ5ЃЉЃЌCЃЈ3ЃЌ5ЃЉЃЛЃЈ2ЃЉЂйSЃНЃ![]() ЃЛЂкEЃЈ1ЃЌ0ЃЉЃЛЃЈ3ЃЉADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдђЕуFМДЮЊЫљЧѓ
ЃЛЂкEЃЈ1ЃЌ0ЃЉЃЛЃЈ3ЃЉADЕФГЄЖШОЭЪЧAF+EFЕФзюаЁжЕЃЌдђЕуFМДЮЊЫљЧѓ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЭЌвЛЦНУцФкЃЌШєвЛИіЕуЕНвЛЬѕжБЯпЕФОрРыВЛДѓгк1ЃЌдђ ГЦетИіЕуЪЧИУжБЯпЕФЁАСкЕуЁБ.дкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕу![]()
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЦНаагк
ЦНаагк![]() жсЃЌВЂНЋ
жсЃЌВЂНЋ![]() НјааЦНвЦЃЌЦНвЦКѓЕу
НјааЦНвЦЃЌЦНвЦКѓЕу![]() ЗжБ№ЖдгІЕу
ЗжБ№ЖдгІЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕу![]() (ЬюаДЪЧЛђВЛЪЧ)жБЯп
(ЬюаДЪЧЛђВЛЪЧ)жБЯп![]() ЕФЁАСкЕуЁБЃЌЧыЫЕУїРэгЩЃЛ
ЕФЁАСкЕуЁБЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєЕу![]() ИеКУТфдкжБЯп
ИеКУТфдкжБЯп![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() Тфдк
Тфдк![]() жсЩЯЃЌЧв
жсЩЯЃЌЧв![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЌХаЖЯЕу
ЕФзјБъЃЌХаЖЯЕу![]() ЪЧЗёЪЧжБЯп
ЪЧЗёЪЧжБЯп![]() ЕФЁАСкЕуЁБЃЌВЂЫЕУїРэгЩЃЎ
ЕФЁАСкЕуЁБЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊвЛДЮКЏЪ§![]() ЕФЭМЯѓЙ§ЕуAЃЈ0ЃЌ3ЃЉКЭЕуBЃЈ3ЃЌ0ЃЉЃЌЧвгые§БШР§КЏЪ§
ЕФЭМЯѓЙ§ЕуAЃЈ0ЃЌ3ЃЉКЭЕуBЃЈ3ЃЌ0ЃЉЃЌЧвгые§БШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕуPЃЎ
ЕФЭМЯѓНЛгкЕуPЃЎ

ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФНтЮіЪНКЭЕуPЕФзјБъЃЎ
ЕФНтЮіЪНКЭЕуPЕФзјБъЃЎ
ЃЈ2ЃЉЛГіСНИіКЏЪ§ ЕФЭМЯѓЃЌВЂжБНгаДГіЕБ![]() ЪБ
ЪБ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉШєЕуQЪЧ![]() жсЩЯвЛЕуЃЌЧвЁїPQBЕФУцЛ§ЮЊ8ЃЌЧѓЕуQЕФзјБъЃЎ
жсЩЯвЛЕуЃЌЧвЁїPQBЕФУцЛ§ЮЊ8ЃЌЧѓЕуQЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвбжЊХзЮяЯпОЙ§Еу A ЃЈЃ2ЃЌ0ЃЉЁЂ B ЃЈ4ЃЌ0ЃЉЁЂ C ЃЈ0ЃЌЃ8ЃЉЃЌХзЮяЯп y ЃН a x 2 ЃЋ b x ЃЋ c ЃЈaЁй0ЃЉгыжБЯп y ЃН x Ѓ4НЛгк B ЃЌ D СНЕуЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНВЂжБНгаДГі D ЕуЕФзјБъЃЛ
ЃЈ2ЃЉЕу P ЮЊХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЧвдкжБЯп BD ЯТЗНЃЌЪдЧѓГіЁї BDP УцЛ§ЕФзюДѓжЕМАДЫЪБЕу P ЕФзјБъЃЛ
ЃЈ3ЃЉЕу Q ЪЧЯпЖЮ BD ЩЯвьгк B ЁЂ D ЕФЖЏЕуЃЌЙ§Еу Q зї QF ЁЭ x жсгкЕу F ЃЌ НЛХзЮяЯпгкЕу G ЃЎ ЕБЁї QDG ЮЊжБНЧШ§НЧаЮЪБЃЌЧѓЕу Q ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЕЭЬМЛЗБЃЃЌТЬЩЋГіааЁБЕФРэФюЕУЕНЙуДѓШКжкЕФНгЪмЃЌдНРДдНЖрЕФШЫЯВЛЖбЁдёздааГЕзїЮЊГіааЙЄОп![]() аЁОќКЭАжАжЭЌЪБДгМвЦяздааГЕШЅЭМЪщЙнЃЌАжАжЯШвд150Уз
аЁОќКЭАжАжЭЌЪБДгМвЦяздааГЕШЅЭМЪщЙнЃЌАжАжЯШвд150Уз![]() ЗжЕФЫйЖШЦяаавЛЖЮЪБМфЃЌанЯЂСЫ5ЗжжгЃЌдйвдmУз/ЗжЕФЫйЖШЕНДяЭМЪщЙнЃЌаЁОќЪМжевдЭЌвЛЫйЖШЦяааЃЌСНШЫааЪЛЕФТЗГЬ
ЗжЕФЫйЖШЦяаавЛЖЮЪБМфЃЌанЯЂСЫ5ЗжжгЃЌдйвдmУз/ЗжЕФЫйЖШЕНДяЭМЪщЙнЃЌаЁОќЪМжевдЭЌвЛЫйЖШЦяааЃЌСНШЫааЪЛЕФТЗГЬ![]() Уз
Уз![]() гыЪБМф
гыЪБМф![]() Зжжг
Зжжг![]() ЕФЙиЯЕШчЭМЃЌЧыНсКЯЭМЯѓЃЌНтД№ЯТСаЮЪЬтЃК
ЕФЙиЯЕШчЭМЃЌЧыНсКЯЭМЯѓЃЌНтД№ЯТСаЮЪЬтЃК

![]() ______ЃЌ
______ЃЌ![]() ______ЃЌ
______ЃЌ![]() ______ЃЛ
______ЃЛ
![]() ШєаЁОќЕФЫйЖШЪЧ120Уз
ШєаЁОќЕФЫйЖШЪЧ120Уз![]() ЗжЃЌЧѓаЁОќдкЭОжагыАжАжЕкЖўДЮЯргіЪБЃЌОрЭМЪщЙнЕФОрРыЃЛ
ЗжЃЌЧѓаЁОќдкЭОжагыАжАжЕкЖўДЮЯргіЪБЃЌОрЭМЪщЙнЕФОрРыЃЛ
![]() дк
дк![]() ЕФЬѕМўЯТЃЌАжАжздЕкЖўДЮГіЗЂжСЕНДяЭМЪщЙнЧАЃЌКЮЪБгыаЁОќЯрОр100УзЃП
ЕФЬѕМўЯТЃЌАжАжздЕкЖўДЮГіЗЂжСЕНДяЭМЪщЙнЧАЃЌКЮЪБгыаЁОќЯрОр100УзЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгЩЫФИіШЋЕШЕФжБНЧШ§НЧаЮЦДГЩЕФДѓе§ЗНаЮЕФУцЛ§ЮЊ84ЃЌжаМфаЁе§ЗНаЮЕФУцЛ§ЮЊ24ЃЌШєжБНЧШ§НЧаЮНЯГЄжБНЧБпЮЊ![]() ЃЌНЯЖЬжБНЧБпЮЊ
ЃЌНЯЖЬжБНЧБпЮЊ![]() ЃЌдђ
ЃЌдђ![]() __ЃЎ
__ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧАыдВOЕФжБОЖЃЌCЁЂDЪЧАыдВOЩЯЕФСНЕуЃЌЧвODЁЮBCЃЌODгыACНЛгкЕуEЃЎ

ЃЈ1ЃЉШєЁЯB=70ЁуЃЌЧѓЁЯCADЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєAB=4ЃЌAC=3ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГАрвЊЙКТђвЛХњРКЧђКЭзуЧђЃЎвбжЊРКЧђЕФЕЅМлБШзуЧђЕФЕЅМлЙѓ40дЊЃЌЛЈ1500дЊЙКТђЕФРКЧђЕФИіЪ§гыЛЈ900дЊЙКТђЕФзуЧђЕФИіЪ§ЧЁКУЯрЕШЃЎ
ЃЈ1ЃЉРКЧђКЭзуЧђЕФЕЅМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉШєИУАрЧЁКУгУЭъ1000дЊЙКТђЕФРКЧђКЭзуЧђЃЌдђЙКТђЕФЗНАИгаФФМИжжЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦяЙВЯэЕЅГЕвбГЩЮЊШЫУЧЯВАЎЕФвЛжжТЬЩЋГіааЗНЪНЃЎвбжЊAЁЂBЁЂCШ§МвЙЋЫОЕФЙВЯэЕЅГЕЖМЪЧАДЦяГЕЪБМфЪеЗбЃЌБъзМШчЯТЃК
ЙЋЫО | ЕЅМлЃЈдЊ/АыаЁЪБЃЉ | ГфжЕгХЛн |
A | m | Гф20дЊЫЭ5дЊЃЌМДЃКГф20дЊЪЕЕУ25дЊ |
B | mЃ0.2 | Юо |
C | 1 | Гф20дЊЫЭ20дЊЃЌМДЃКГф20дЊЪЕЕУ40дЊ |
ЃЈзЂЃКЪЙгУетШ§МвЙЋЫОЕФЙВЯэЕЅГЕЃЌВЛзуАыаЁЪБОљАДАыаЁЪБМЦЗбЃЎгУЛЇЕФеЫЛЇгрЖюГЄЦкгааЇЃЌЕЋВЛПЩЬсЯжЃЎЃЉ
4дТГѕЃЌРюУїзЂВсГЩСЫAЙЋЫОЕФгУЛЇЃЌеХКьзЂВсГЩСЫBЙЋЫОЕФгУЛЇЃЌВЂЧвСНШЫдкИїздеЫЛЇЩЯЗжБ№ГфжЕ20дЊЃЎвЛИідТЯТРДЃЌРюУїЁЂеХКьСНШЫЪЙгУЕЅГЕЕФДЮЪ§ЧЁКУЯрЭЌЃЌЧвУПДЮЖМдкАыаЁЪБвдФкЃЌНсЙћЕНдТЕзРюУїЁЂеХКьЕФеЫЛЇгрЖюЗжБ№ЯдЪОЮЊ5дЊЁЂ8дЊЃЎ
ЃЈ1ЃЉЧѓmЕФжЕЃЛ
ЃЈ2ЃЉ5дТЗнЃЌCЙЋЫОдкдБъзМЕФЛљДЁЩЯгжЭЦГіаТгХЛнЃКУПдТЕФдТГѕИјгУЛЇЫЭГі5еХУтЗбЪЙгУШЏЃЈ1
ДЮгУГЕжЛФмЪЙгУ1еХШЏЃЉЃЎШчЙћЭѕРкУПдТЪЙгУЕЅГЕЕФДЮЪ§ЯрЭЌЃЌЧвдк30ДЮвдФкЃЌУПДЮгУГЕЖМВЛГЌЙ§
АыаЁЪБ. ШєвЊдкетШ§МвЙЋЫОжабЁдёвЛМвВЂГфжЕ20дЊЃЌНіДгзЪЗбНЧЖШПМТЧЃЌЧыФуАяЫћзїГібЁдёЃЌВЂЫЕ
УїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com