
【题目】如图,已知A(-1,0),B(1,0),C为y轴正半轴上一点,点D为第三象限一动点,CD交AB于F,且∠ADB=2∠BAC,

(1)求证:∠ADB与∠ACB互补;
(2)求证:CD平分∠ADB;
(3)若在D点运动的过程中,始终有DC=DA+DB,在此过程中,∠BAC的度数是否变化?如果变化,请说明理由;如果不变,请求出∠BAC的度数.
【答案】(1)证明见解析;(2)证明见解析;(3)∠BAC=60°.
【解析】
(1)先判断△ABC是等腰三角形,然后在△ABC中利用三角形内角和定理以及∠ADB=2∠BAC即可得到结论;
(2)过点C作AM⊥DA于点M,作CN⊥BD于点N,运用“AAS”证明△CAM≌△CBN得CM=CN,根据“到角的两边距离相等的点在角的平分线上”得证;
(3)延长DB至点P,使BP=AD,连接CP,则可得CD=DP,证明△CAD≌△CBP,从而可得 △CDP是等边三角形,从而求∠BAC的度数.
(1)∵A(-1,0),B(1,0),
∴OA=OB=1,
∵CO⊥AB,
∴CA=CB,
∴∠ABC=∠BAC,
∵∠ABC+∠BAC+∠ACB=180°,∠ADB=2∠BAC,
∴∠ADB+∠ACB=180°,
即∠ADB与∠ACB互补;
(2)过点C作AM⊥DA于点M,作CN⊥BD于点N,则∠AMC=∠ANB=90°,

∵∠ADB+∠AMC+∠ANB+∠MCN=360°,
∴∠ADB+∠MCN=180°,
又∵∠ADB+∠ACB=180°,
∴∠MCN=∠ACB,
∴∠MCN-∠CAN=∠ACB-∠CAN,
即∠ACM=∠BCN,
又∵AB=AC,
∴△ACM≌△ABN (AAS),
∴AM=AN.
∴CD平分∠ADB(到角的两边距离相等的点在角的平分线上);
(3)∠BAC的度数不变化,
延长DB至点P,使BP=AD,连接CP,

∵CD=AD+BD,
∴CD=DP,
∵∠ADB+∠DBC+∠ACB+∠CAD=360°,∠ADB+∠ACB=180°,
∴∠CAD+∠CBD=180°,
∵∠CBD+∠CBP=180°,
∴∠CAD=∠CBP,
又∵CA=CB,
∴△CAD≌△CBP,
∴CD=CP,
∴CD=DP=CP,即△CDP是等边三角形,
∴∠CDP=60°,
∴∠ADB=2∠CDP=120°,
又∵∠ADB=2∠BAC,
∴∠BAC=60°.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数y=﹣![]() x2+2x+5 图象的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为( )
x2+2x+5 图象的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为( )
A. 0米到8米 B. 5米到8米 C. ![]() 到8米 D. 5米到
到8米 D. 5米到![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一座抛物线形拱桥,正常水位桥下面宽度为20米,拱顶距离水平面4米,如图建立直角坐标系,若正常水位时,桥下水深6米,为保证过往船只顺利航行,桥下水面宽度不得小于18米,则当水深超过多少米时,就会影响过往船只的顺利航行( )

A. 2.76米 B. 6.76米 C. 6米 D. 7米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为![]() ,则a、b的值分别为( )
,则a、b的值分别为( )

A. ![]() ,
,![]() B.
B. ![]() ,﹣
,﹣![]() C.
C. ![]() ,﹣
,﹣![]() D. ﹣
D. ﹣![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx+1与抛物线y=x2-4x
(1)求证:直线l与该抛物线总有两个交点;
(2)设直线l与该抛物线两交点为A,B,O为原点,当k=-2时,求△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+4x.
(1)写出二次函数y=﹣x2+4x图象的对称轴;
(2)在给定的平面直角坐标系中,画出这个函数的图象(列表、描点、连线);
(3)根据图象,写出当y<0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC与△ADE中,∠BAC=∠DAE=90°,AD=AE,AB=AC,且B、D、E三点在一条直线上.
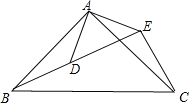
(1)求证:BD=CE.
(2)求∠BEC的度数.
(3)写出BE与AE、CE的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为2,则AC的长是( )

A. ![]() B.
B. ![]() C. 5 D.
C. 5 D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com