
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=1,下列结论:①2a+b=0;②9a+c>3b;③若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y3<y2:④若方程ax2+bx+c=﹣3(a≠0)的两根为x1和x2,且x1<x2,则x1<﹣1<3<x2;⑤m(am+b)﹣b<a.其中正确的结论有( )
,y3)在该函数图象上,则y1<y3<y2:④若方程ax2+bx+c=﹣3(a≠0)的两根为x1和x2,且x1<x2,则x1<﹣1<3<x2;⑤m(am+b)﹣b<a.其中正确的结论有( )
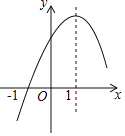
A.1个B.2个C.3个D.4个
【答案】C
【解析】
根据对称轴为x=1,再结合对称轴公式即可判断①;当x=﹣3时,y<0,代入即可判断②;找出(![]() ,y3)关于直线x=1的对称点即可判断③;设y=ax2+bx+c,y=﹣3,根据图象可判断④;当x=1时,a+b+c为最大值,可判断⑤.
,y3)关于直线x=1的对称点即可判断③;设y=ax2+bx+c,y=﹣3,根据图象可判断④;当x=1时,a+b+c为最大值,可判断⑤.
解:①由题意可知:对称轴x=1,
∴![]() =1,
=1,
∴2a+b=0,故①正确;
②当x=﹣3时,y<0,
∴y=9a﹣3b+c<0,故②错误;
③(![]() ,y3)关于直线x=1的对称点为(
,y3)关于直线x=1的对称点为(![]() ,y3),
,y3),
由图可知:x<1时,y随着x的增大而减小,
由于﹣3<![]() <
<![]() ,
,
∴y1<y3<y2,故③正确;
④设y=ax2+bx+c,y=﹣3,
由于图象可知:直线y=﹣3与抛物线y=ax2+bx+c有两个交点,
∴方程ax2+bx+c=﹣3(a≠0)的两根为x1和x2,
∴x1<﹣1<3<x2,故④正确;
⑤当x=1时,y=a+b+c,此时a+b+c为最大值,
当x=m时,y=am2+bm+c,
∴am2+bm+c≤a+b+c,
即m(am+b)﹣b≤a,故⑤错误;
故选:C.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
【题目】某商店销售 A、B 两种品牌的彩色电视机,A、B 两种彩电的进价每台分别为2000 元、1600元.一 月 份 A、B 两 种 彩 电 每 台 销 售 价 分 别 为 2700 元、2100 元,月 利 润 为 12000元.为了增加利润,二月份营销人员提供了两种销售策略:
策略一: A 种彩电每台降价100元,B 种彩电每台降价80元,估计月销售量分别增长30%、40%;
策略二: A 种彩电每台降价 150 元,B 种彩电每台降价 100 元,估计月销售量都增长50%.
根据以上信息完成下列各题:
(1)求一月份 A、B 两种彩电的销售量.
(2)二月份这两种策略是否能增加利润?
(3)二月份该商店应该采用上述两种销售策略中的哪一种,方能使商店所获得的利润较多?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市欲购进一种今年新上市的产品,购进价为20元![]() 件,为了调查这种新产品的销路,该超市进行了试销售,得知该产品每天的销售量
件,为了调查这种新产品的销路,该超市进行了试销售,得知该产品每天的销售量![]() 件
件![]() 与每件的销售价
与每件的销售价![]() 元
元![]() 件
件![]() 之间有如下关系:
之间有如下关系:![]()
![]() 请写出该超市销售这种产品每天的销售利润
请写出该超市销售这种产品每天的销售利润![]() 元
元![]() 与x之间的函数关系式,并求出超市能获取的最大利润是多少元.
与x之间的函数关系式,并求出超市能获取的最大利润是多少元.
![]() 若超市想获取1500元的利润
若超市想获取1500元的利润![]() 求每件的销售价.
求每件的销售价.
![]() 若超市想获取的利润不低于1500元,请求出每件的销售价X的范围?
若超市想获取的利润不低于1500元,请求出每件的销售价X的范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年“519(我要走)全国徒步日(江夏站)”暨第六届“环江夏”徒步大会5月19日在美丽的花山脚下降重举行.组委会(活动主办方)为了奖励活动中取得了好成绩的参赛选手,计划购买共100件的甲、乙两种纪念品发放.其中甲种纪念品每件售价120元,乙种纪念品每件售价80元.
(1)如果购买甲、乙两种纪念品一共花费了9600元,求购买甲、乙两种纪念品各是多少件?
(2)设购买甲种纪念品![]() 件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
件,如果购买乙种纪念品的件数不超过甲种纪念品的数量的2倍,并且总费用不超过9400元.问组委会购买甲、乙两种纪念品共有几种方案?哪一种方案所需总费用最少?最少总费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:(一)如果两个函数y1,y2,存在x取同一个值,使得y1=y2,那么称y1,y2为“合作函数”,称对应x的值为y1,y2的“合作点”;
(二)如果两个函数为y1,y2为“合作函数”,那么y1+y2的最大值称为y1,y2的“共赢值”.
(1)判断函数y=x+2m与y=![]() 是否为“合作函数”,如果是,请求出m=1时它们的合作点;如果不是,请说明理由;
是否为“合作函数”,如果是,请求出m=1时它们的合作点;如果不是,请说明理由;
(2)判断函数y=x+2m与y=3x﹣1(|x|≤2)是否为“合作函数”,如果是,请求出合作点;如果不是,请说明理由;
(3)已知函数y=x+2m与y=x2﹣(2m+1)x+(m2+4m﹣3)(0≤x≤5)是“合作函数”,且有唯一合作点.
①求出m的取值范围;
②若它们的“共赢值”为24,试求出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的内切圆
的内切圆![]() 与
与![]() ,
,![]() ,
,![]() 分别相切于点
分别相切于点![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,点
,点![]() 在射线
在射线![]() 上运动,过点
上运动,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
(1)直接写出线段![]() ,
,![]() 及
及![]() 半径的长:
半径的长:
(2)设![]() ,
,![]() . 求
. 求![]() 关于
关于![]() 的函数关系式:
的函数关系式:
(3)当![]() 与
与![]() 相切时,求相应的
相切时,求相应的![]() 值.
值.
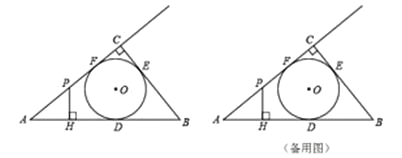
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=2,BC=3.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于![]() PQ的长为半径画弧,两弧相交于点N,射线CN交AD与点F,交BA的延长线于点E,则三角形CDF与四边形AFCB的面积比是( )
PQ的长为半径画弧,两弧相交于点N,射线CN交AD与点F,交BA的延长线于点E,则三角形CDF与四边形AFCB的面积比是( )
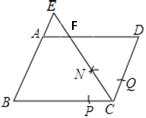
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校为创建书香校园,4月份购进一批图书,经了解,科普书的单价比文学书的单价多4元,用1500元购进的科普书与1000元购进的文学书本数相等.
(1)求4月份购进的科普书和文学书的单价各是多少元?
(2)若5月份科普书和文学书的单价与4月份相比保持不变,我校现打算用1250元再购进一批科普书和文学书,问购进科普书65本后至多还能购进多少本文学书?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com