
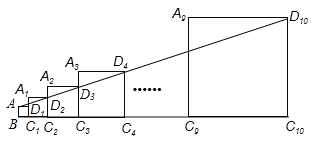
【题目】已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推…,若A1C1=2,且点A,D2, D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是______
【答案】![]() .
.
【解析】试题解析:延长D4A和C1B交于O,
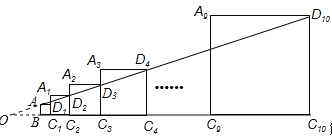
∵AB∥A2C1,
∴△AOB∽△D2OC2,
∴![]() ,
,
∵AB=BC1=1,D 2C2=C1C2=2,
∴![]()
∴OC2=2OB,
∴OB=BC2=3,
∴OC2=6,
设正方形A2C2C3D3的边长为x1,
同理证得:△D2OC2∽△D3OC3,
∴![]() ,解得,x1=3,
,解得,x1=3,
∴正方形A2C2C3D3的边长为3,
设正方形A3C3C4D4的边长为x2,
同理证得:△D3OC3∽△D4OC4,
∴![]() ,解得x2=
,解得x2=![]() ,
,
∴正方形A3C3C4D4的边长为![]() ;
;
设正方形A4C4C5D5的边长为x3,
同理证得:△D4OC4∽△D5OC5,
∴ ,解得x=
,解得x=![]() ,
,
∴正方形A4C4C5D5的边长为![]() ;
;
以此类推….
正方形An-1Cn-1CnDn的边长为![]() ;
;
∴正方形A9C9C10D10的边长为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4![]() ,
, ![]()
(1)求AC所在直线的解析式;
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=3,若点M,N分别在OA,OB上,ΔPMN为等边三角形,则满足上述条件的△PMN有中( )

A. 1个B. 2个C. 3个D. 3个以上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有9个黄球,13个黑球,11个红球,它们除颜色外其余都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取出若干个黄球,井放入相同数量的黑球,若要使搅拌均与后从袋中摸出一个球是黑球的概率不小于![]() ,问至少要取出多少个黄球?
,问至少要取出多少个黄球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】★若两个扇形满足弧长的比等于它们半径的比,则称这两个扇形相似.如图,如果扇形AOB与扇形A1O1B1是相似扇形,且半径OA∶O1A1=k(k为不等于0的常数).那么下面四个结论:①∠AOB=∠A1O1B1;②△AOB∽△A1O1B1;③![]() =k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )
=k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
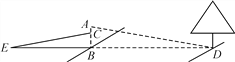
【题目】某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).
①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;
②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB延长线上的点E处,此时小亮测得BE=9.6米,小明的眼睛距地面的距离CB=1.2米.
根据以上测量过程及测量数据,请你求出河宽BD是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,则AD等于( )
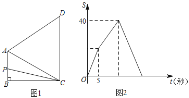
A. 10B. ![]() C. 8D.
C. 8D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com