
【题目】如图,四边形ABCD内接于⊙O,∠BAD=90°, ![]() =
= ![]() ,过点C作CE⊥AD,垂足为E,若AE=3,DE=
,过点C作CE⊥AD,垂足为E,若AE=3,DE= ![]() ,求∠ABC的度数.
,求∠ABC的度数.
 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
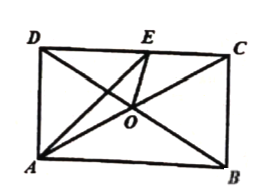
【题目】如图,在矩形![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,给出以下结论:①
,给出以下结论:①![]() 为等腰直角三角形;②
为等腰直角三角形;②![]() 为等边三角形;③
为等边三角形;③![]() ;④
;④![]() ⑤
⑤![]() 是
是![]() 的中位线.其中正确的结论有( )
的中位线.其中正确的结论有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区果农收获草莓30吨,枇杷13吨,现计划租用甲、乙两种货车共10辆将这批水果全部运往省城,已知甲种货车可装草莓4吨和枇杷1吨,乙种货车可装草莓、枇杷各2吨.
(1)该果农安排甲、乙两种货车时有几种方案请您帮助设计出来;
(2)若甲种货车每辆要付运输费2 000元,乙种货车每辆要付运输费1 300元,则该果农应选择哪种运输方案才能使运费最少,最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
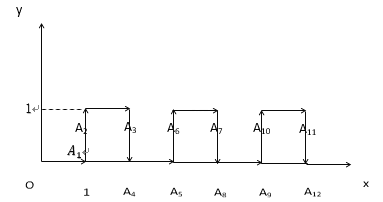
【题目】在平面直角坐标系中,一个智能机器人接到如下指令,从原点O出发,按向右、向上、向右、向下的方向依次不断移动,每次移动1个单位长度,其行走的路线如图所示,第1次移动到A1,第2次移动到A2……,第n次移动到An,则三角形OA2A2018的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com