Question

2．如图，在四边形ABCD中，线段CE交四边形的边于点E，点H为BD中点，BF，DG分别垂直CE于点F和点G，连接HF，HG．
（1）如图1，若四边形ABCD为正方形，AB=3，AE=2EB，求BF的长；
（2）如图1，若四边形ABCD为正方形，试猜想FG与HF的数量关系，并说明理由；
（3）如图2，若四边形ABCD为平行四边形，CE平分∠BCD且交AD于点E，其他条件不变，求证：AE=HF+HG．

Answer 1

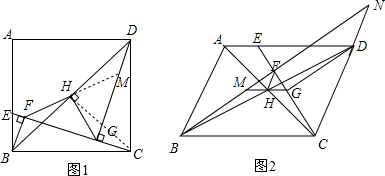
分析 （1）利用面积法来求BF的长度；
（2）通过全等三角形的判定与性质得到△BFC≌△CGD、△HBF≌△HCG，则推知△FGH为等腰直角三角形，所以FG=$\sqrt{2}$HF；
（3）延长GH交BF于点M．由全等三角形的判定定理推知△BHM≌△DHG，则由该全等三角形的性质、直角三角形斜边上中线的性质证得FH=GH=MH，易证：AH=HC，EG=GC，所以AE=2HG，故AE=HF+HG．

解答 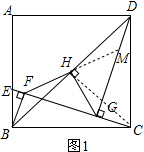解：（1）如图1，∵四边形ABCD为正方形，AB=3，AE=2EB，
∴BC=AB=3，AE=2，BE=1，
∴在直角△BEC中，由勾股定理得到：CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
则$\frac{1}{2}$BE•BC=$\frac{1}{2}$CE•BF，
故BF=$\frac{BE•BC}{CE}$=$\frac{1×3}{\sqrt{10}}$=$\frac{3\sqrt{10}}{10}$；

（2）如图1，FG=$\sqrt{2}$HF．理由如下：
∵在△BFC与△CGD中，$\left\{\begin{array}{l}{∠BCF=∠CDG}\\{∠BFC=∠CGD}\\{BC=CD}\end{array}\right.$，
∴△BFC≌△CGD（AAS），
∴BF=CG，∠FBC=∠DCG．
∵点H是BD的中点，
∴CH⊥BD，且HC=BH=DH，
∴∠HBC=∠HCD=45°，
∴∠FBH=∠GHC．
∵在△HBF与△HCG中，$\left\{\begin{array}{l}{BF=CG}\\{∠FBH=∠GCH}\\{BH=CH}\end{array}\right.$，
∴△HBF≌△HCG（SAS），
∴FH=GH，∠FHB=∠GHC，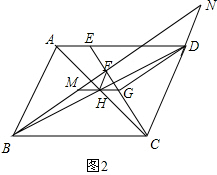
∴∠FHG=∠BHC=90°，
∴FG=$\sqrt{2}$HF；

（3）证明：如图2，∵BF，DG分别垂直CE于点F和点G，
∴BF∥DG．
又∵BH=HD，
∴∠MHB=∠GDH．
∵在△BHM与△DHG中，$\left\{\begin{array}{l}{∠MBH=∠GDH}\\{BH=DH}\\{∠MHB=∠GHD}\end{array}\right.$，
∴△BHM≌△DHG（ASA），
∴HM=HG．
∵∠MFG=90°，
∴FH=GH=MH，
易证AH=HC，EG=GC，
∴AE=2HG，
故AE=HF+HG．

点评 本题综合考查了等腰三角形的判定与性质、正方形（平行四边形的性质以及全等三角形的判定与性质，熟记以上图形的性质并能灵活运用其性质是解答本题的关键，综合性较强，难度较大．