
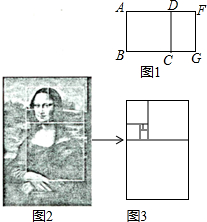
 数学中,把长与宽之比为$\frac{{\sqrt{5}+1}}{2}$(或宽与长之比为$\frac{{\sqrt{5}-1}}{2}$)的矩形称为黄金矩形.思考解决下列问题:
数学中,把长与宽之比为$\frac{{\sqrt{5}+1}}{2}$(或宽与长之比为$\frac{{\sqrt{5}-1}}{2}$)的矩形称为黄金矩形.思考解决下列问题:分析 (1)由黄金矩形的定义可得:$\frac{AB}{AF}$=$\frac{{\sqrt{5}-1}}{2}$,将AF=1代入,计算即可求出AB的长;
(2)利用AB=DC=AD和$\frac{AB}{AF}$=$\frac{{\sqrt{5}-1}}{2}$,通过等量代换,求得$\frac{FD}{CD}$=$\frac{{\sqrt{5}-1}}{2}$,得到矩形DCGF是黄金矩形;
(3)由$\frac{AB}{AF}$=$\frac{{\sqrt{5}-1}}{2}$,可得AB=$\frac{{\sqrt{5}-1}}{2}$AF,即CD=FG=$\frac{{\sqrt{5}-1}}{2}$AF,即以黄金矩形的宽为边向矩形内部做正方形,产生的小矩形的长为原来矩形长的$\frac{{\sqrt{5}-1}}{2}$,由图可知,一共作正方形6次,所以最小黄金矩形的长是($\frac{{\sqrt{5}-1}}{2}$)6a.
解答 解:(1)由题意可得:$\frac{AB}{AF}$=$\frac{{\sqrt{5}-1}}{2}$,
又∵AF=1,
∴AB=$\frac{{\sqrt{5}-1}}{2}$; (2)留下的矩形DCGF是黄金矩形.理由如下:
(2)留下的矩形DCGF是黄金矩形.理由如下:
∵四边形ABCD是正方形,
∴AB=DC=AD,
又∵$\frac{AB}{AF}$=$\frac{{\sqrt{5}-1}}{2}$,
∴$\frac{AD}{AF}$=$\frac{{\sqrt{5}-1}}{2}$,
即点D是线段AF的黄金分割点,$\frac{FD}{AD}$=$\frac{{\sqrt{5}-1}}{2}$,
∴$\frac{FD}{CD}$=$\frac{{\sqrt{5}-1}}{2}$,
∴矩形DCGF是黄金矩形;
(3)若图3中最大黄金矩形的长为a,由题意,可得最小黄金矩形的长是($\frac{{\sqrt{5}-1}}{2}$)6a.
点评 本题考查了黄金分割:把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值($\frac{\sqrt{5}-1}{2}$)叫做黄金比.理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键.


科目:初中数学 来源: 题型:填空题
 如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1.则弧BD的长是$\frac{2\sqrt{3}π}{9}$.
如图,以AB为直径的⊙O与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1.则弧BD的长是$\frac{2\sqrt{3}π}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
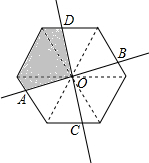 如图,正六边形中,点A在一边上运动,AO交六边形的另一边于B,过O作AB的垂线交六边形于C,D,形成如图所示的阴影部分.小姜设计了两个方案:①把如图所示的飞镖盘纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是$\frac{1}{4}$.②以O为旋转中心,把六边形做成转盘,则指针落在阴影部分的概率是$\frac{1}{4}$.那么以上两种方案正确的是( )
如图,正六边形中,点A在一边上运动,AO交六边形的另一边于B,过O作AB的垂线交六边形于C,D,形成如图所示的阴影部分.小姜设计了两个方案:①把如图所示的飞镖盘纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是$\frac{1}{4}$.②以O为旋转中心,把六边形做成转盘,则指针落在阴影部分的概率是$\frac{1}{4}$.那么以上两种方案正确的是( )| A. | ①② | B. | ① | C. | ② | D. | ①②都错误 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
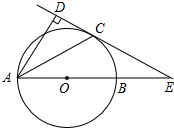 如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
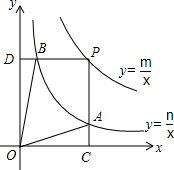 函数y=$\frac{m}{x}$和y=$\frac{n}{x}$在第一象限内的图象如图,点P是y=$\frac{m}{x}$的图象上一点,PC⊥x轴于点C,交y=$\frac{n}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{n}{x}$的图象于点B,且PA=3CA,tan∠DOB=$\frac{1}{5}$,SOAPB=3,则点B的坐标为($\frac{\sqrt{5}}{5}$,$\sqrt{5}$).
函数y=$\frac{m}{x}$和y=$\frac{n}{x}$在第一象限内的图象如图,点P是y=$\frac{m}{x}$的图象上一点,PC⊥x轴于点C,交y=$\frac{n}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{n}{x}$的图象于点B,且PA=3CA,tan∠DOB=$\frac{1}{5}$,SOAPB=3,则点B的坐标为($\frac{\sqrt{5}}{5}$,$\sqrt{5}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
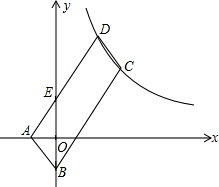 如图,平行四边形ABCD的顶点A,B的坐标分别是A(-2,0),B(0,-4),顶点C,D在双曲线y=$\frac{k}{x}$上,边AD交y轴于E点,且四边形BCDE的面积是△ABE面积的5倍,则k=48.
如图,平行四边形ABCD的顶点A,B的坐标分别是A(-2,0),B(0,-4),顶点C,D在双曲线y=$\frac{k}{x}$上,边AD交y轴于E点,且四边形BCDE的面积是△ABE面积的5倍,则k=48.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是小明在使用央视记者柴静关于雾霾调查纪录片《穹顶之下》中推荐的APP时的一张截图.它显示的是杭州10个地区的空气质量情况,你觉得用以下哪个统计量来表示整个杭州市的空气质量情况较合适.( )
如图是小明在使用央视记者柴静关于雾霾调查纪录片《穹顶之下》中推荐的APP时的一张截图.它显示的是杭州10个地区的空气质量情况,你觉得用以下哪个统计量来表示整个杭州市的空气质量情况较合适.( )| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 以上都可以 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com