
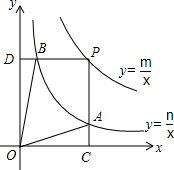
 函数y=$\frac{m}{x}$和y=$\frac{n}{x}$在第一象限内的图象如图,点P是y=$\frac{m}{x}$的图象上一点,PC⊥x轴于点C,交y=$\frac{n}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{n}{x}$的图象于点B,且PA=3CA,tan∠DOB=$\frac{1}{5}$,SOAPB=3,则点B的坐标为($\frac{\sqrt{5}}{5}$,$\sqrt{5}$).
函数y=$\frac{m}{x}$和y=$\frac{n}{x}$在第一象限内的图象如图,点P是y=$\frac{m}{x}$的图象上一点,PC⊥x轴于点C,交y=$\frac{n}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{n}{x}$的图象于点B,且PA=3CA,tan∠DOB=$\frac{1}{5}$,SOAPB=3,则点B的坐标为($\frac{\sqrt{5}}{5}$,$\sqrt{5}$). 分析 根据反比例函数系数k的几何意义得出SOCPD=m,S△OBD=$\frac{1}{2}$n,S△AOC=$\frac{1}{2}$n,进而得出SOAPB=SOCPD-S△OBD-S△AOC=m-n=3,根据PA=3CA,得出$\frac{1}{2}$m=4×$\frac{1}{2}$n,即m=4n,解$\left\{\begin{array}{l}{m-n=3}\\{m=4n}\end{array}\right.$得$\left\{\begin{array}{l}{m=4}\\{n=1}\end{array}\right.$,求得点B在y=$\frac{1}{x}$图象上,所以设B(a,$\frac{1}{a}$),根据tan∠DOB=$\frac{a}{\frac{1}{a}}$=$\frac{1}{5}$,求得a=$\frac{\sqrt{5}}{5}$,即可求得B的坐标.
解答 解:∵点P是y=$\frac{m}{x}$的图象上一点,
∴SOCPD=m,
∵点A、点B是y=$\frac{n}{x}$的图象上一点,
∴S△OBD=$\frac{1}{2}$n,S△AOC=$\frac{1}{2}$n,
∴SOAPB=SOCPD-S△OBD-S△AOC=m-n=3,
连接OP,
∵PA=3CA,
∴S△OPC=4S△OAC,
∴$\frac{1}{2}$m=4×$\frac{1}{2}$n,
∴m=4n,
解$\left\{\begin{array}{l}{m-n=3}\\{m=4n}\end{array}\right.$得$\left\{\begin{array}{l}{m=4}\\{n=1}\end{array}\right.$,
∴点B在y=$\frac{1}{x}$图象上,
设B(a,$\frac{1}{a}$),
∴BD=a,OD=$\frac{1}{a}$,
∵tan∠DOB=$\frac{1}{5}$,
∴$\frac{BD}{OD}$=$\frac{1}{5}$,即$\frac{a}{\frac{1}{a}}$=$\frac{1}{5}$,
解得a=$\frac{\sqrt{5}}{5}$,
∴B($\frac{\sqrt{5}}{5}$,$\sqrt{5}$).
故答案为($\frac{\sqrt{5}}{5}$,$\sqrt{5}$).
点评 本题考查了反比例函数图象上点的坐标特征,反比例函数系数k的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积等于|k|;反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S=$\frac{1}{2}$|k|.该知识点是中考的重要考点,同学们应高度关注.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
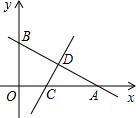 如图,一次函数y=-$\frac{2}{3}$x+b的图象与x轴、y轴分别交于点A、B,线段AB的中点为D(3,2).将△AOB沿直线CD折叠,使点A与点B重合,直线CD与x轴交于点C.
如图,一次函数y=-$\frac{2}{3}$x+b的图象与x轴、y轴分别交于点A、B,线段AB的中点为D(3,2).将△AOB沿直线CD折叠,使点A与点B重合,直线CD与x轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
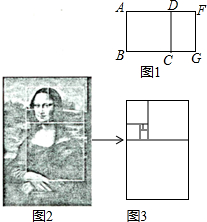 数学中,把长与宽之比为$\frac{{\sqrt{5}+1}}{2}$(或宽与长之比为$\frac{{\sqrt{5}-1}}{2}$)的矩形称为黄金矩形.思考解决下列问题:
数学中,把长与宽之比为$\frac{{\sqrt{5}+1}}{2}$(或宽与长之比为$\frac{{\sqrt{5}-1}}{2}$)的矩形称为黄金矩形.思考解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
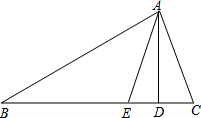 如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=30°,∠DAE=20°,
如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=30°,∠DAE=20°,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
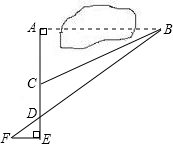 数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:
数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A、B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E,再从E沿着垂直于AE的方向走到F,C为AE上一点,其中3位同学分别测得三组数据:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com