
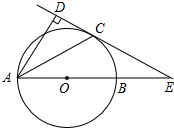
 如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.分析 (1)如图,连接OC,由AC平分∠DAB得到∠DAC=∠CAB,然后利用等腰三角形的性质得到∠OCA=∠CAB,接着利用平行线的判定得到AD∥CO,而CD⊥AD,由此得到CD⊥AD,最后利用切线的判定定理即可证明CD为⊙O的切线;
(2)由BE=OB,AB=2BE得到BO=BE=CO,设BO=BE=CO=x,所以OE=2x,在Rt△OCE中,利用勾股定理列出关于x的方程,解方程求出x,最后利用三角函数的定义即可求解.
解答 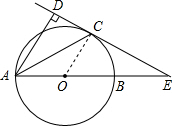 (1)证明:连接OC,
(1)证明:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC=∠DAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥CD,
∴CD⊥OC,
∴CD为⊙O的切线;
(2)解:设OC=OB=BE=x,则OE=2OC,
∴∠E=30°
在Rt△OCE中,x2+${\sqrt{3}^2}$=4x2,
x=1,
∴AE=3,
∴AD=$\frac{1}{2}$AE=$\frac{3}{2}$.
点评 此题主要考查了切线的判定与性质,同时也利用了圆周角定理及勾股定理,首先利用切线的判定证明切线,然后利用切线的性质、勾股定理列出方程解决问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
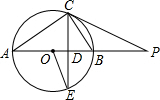 如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连结OE、AC,已知∠POE=2∠CAB,∠P=∠E.
如图,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点D.连结OE、AC,已知∠POE=2∠CAB,∠P=∠E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -(-a)4÷a2=-a2 | B. | (2a+3b)(2a-3b)=2a2-3b2 | ||
| C. | (xy)-1($\frac{1}{2}$xy)2=$\frac{1}{4}$xy2 | D. | 3ab-2ab=1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
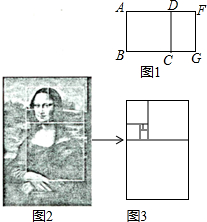 数学中,把长与宽之比为$\frac{{\sqrt{5}+1}}{2}$(或宽与长之比为$\frac{{\sqrt{5}-1}}{2}$)的矩形称为黄金矩形.思考解决下列问题:
数学中,把长与宽之比为$\frac{{\sqrt{5}+1}}{2}$(或宽与长之比为$\frac{{\sqrt{5}-1}}{2}$)的矩形称为黄金矩形.思考解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com