
【题目】已知:⊙O是△ABC的外接圆,∠OAB=40°,则∠ACB的大小为( )
A.20°
B.50°
C.20°或160°
D.50°或130°
【答案】D
【解析】解: 
∵OA=OB,
∴∠OBA=∠OAB=40°,
∴∠AOB=180°﹣∠OAB﹣∠OBA=100°,
∴∠ACB= ![]() ∠AOB=50°.
∠AOB=50°.
当点C在点C′的位置时,∠AC′B=180°﹣50°=130°.
所以答案是:D.
【考点精析】本题主要考查了圆周角定理和圆内接四边形的性质的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形才能正确解答此题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】某水果店计划进A,B两种水果共140千克,这两种水果的进价和售价如表所示
进价 | 售价 | |
A种水果 | 5 | 8 |
B种水果 | 9 | 13 |
![]() 若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
若该水果店购进这两种水果共花费1020元,求该水果店分别购进A,B两种水果各多少千克?
![]() 在
在![]() 的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价
的基础上,为了迎接春节的来临,水果店老板决定把A种水果全部八折出售,B种水果全部降价![]() 出售,那么售完后共获利多少元?
出售,那么售完后共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂工人小李生产A、B两种产品.若生产A产品10件,生产B产品10件,共需时间350分钟;若生产A产品30件,生产B产品20件,共需时间850分钟.
(1)小李每生产一件![]() 种产品和每生产一件
种产品和每生产一件![]() 种产品分别需要多少分钟;
种产品分别需要多少分钟;
(2)小李每天工作8个小时,每月工作25天.如果小李四月份生产![]() 种产品
种产品![]() 件(
件(![]() 为正整数).
为正整数).
①用含![]() 的代数式直接表示小李四月份生产
的代数式直接表示小李四月份生产![]() 种产品的件数;
种产品的件数;
②已知每生产一件![]() 产品可得1.40元,每生产一件
产品可得1.40元,每生产一件![]() 种产品可得2.80元,若小李四月份的工资不少于1500元,求
种产品可得2.80元,若小李四月份的工资不少于1500元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠5=∠6,∠3=∠4,试说明AE∥BD,AD∥BC.请完成下列证明过程.
证明:
∵∠5=∠6,
∴AB∥CE( ),
∴∠3=__________
∵∠3=∠4,
∴∠4=∠BDC( ),
∴ ∥BD( ),
∴∠2= ( )
∵∠1=∠2,
∴∠1=______,
∴AD∥BC

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市场上的红茶由茶原液与纯净水按一定比例配制而成,其中购买一吨茶原液的钱可以买15 吨纯净水。由于今年以来茶产地连续大旱,茶原液收购价上涨50%.纯净水价也上涨了10%,导致配制的这种茶饮料成本上涨40%,问这种茶饮料中茶原液与纯净水的配制比例为_______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段a和射线OA,射线OA上有点B.

(1)用圆规和直尺在射线OA上作线段CD,使点B为CD的中点,点C在点B的左边,且BC=a.(不用写作法,保留作图痕迹)
(2)在(1)的基础上,若OB=12cm,OC=5cm,求线段OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在 ![]() 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 ![]() 处飞出(
处飞出( ![]() 在
在 ![]() 轴上),运动员孙可在距
轴上),运动员孙可在距 ![]() 点6米的
点6米的 ![]() 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ![]() ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.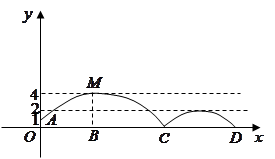
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点 ![]() 距守门员多少米?(取
距守门员多少米?(取 ![]() )
)
(3)孙可要抢到足球第二个落地点 ![]() ,他应从第一次落地点
,他应从第一次落地点 ![]() 再向前跑多少米?(取
再向前跑多少米?(取 ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com