
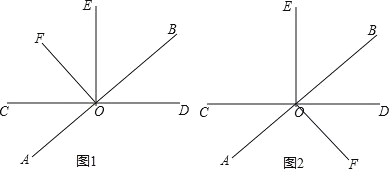
【题目】已知如图,直线![]() 相交于点
相交于点![]() .
.
(1)若∠AOC=35°,求![]() 的度数;
的度数;
(2)若∠BOD:∠BOC=2:4,求![]() 的度数;
的度数;
(3)在(2)的条件下,过点![]() 作
作![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)55°,(2)150°,(3)60°或120°
【解析】
(1)根据AOB共线即可知![]() +
+![]() +
+![]() =180°即可解得;
=180°即可解得;
(2)根据平角的定义可求出∠BOD,根据对顶角的定义可求出∠AOC,再根据角的和差关系可求∠AOE的度数;
(3)先过点O作![]() ,再分两种情况根据角的和差关系来求∠EOF即可.
,再分两种情况根据角的和差关系来求∠EOF即可.
(1)∵∠AOC=35°,![]() ,
,
∴![]() =180°-
=180°-![]() -
-![]() =55°;-
=55°;-
(2)∵∠BOD:∠BOC=2:4,
∴![]() =180°×
=180°×![]() =60°,
=60°,
∴∠AOC=60°,
∴∠AOE=60°+90°=150°;
(3)如图1,∠EOF=150°-90°=60°,
或如图2,∠EOF=360°-150°-90°=120°,
故∠EOF的度数为60°或120°.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
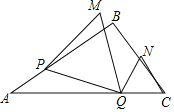
【题目】如图,在△ABC中,AB=7.5,AC=9,S△ABC=![]() .动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
.动点P从A点出发,沿AB方向以每秒5个单位长度的速度向B点匀速运动,动点Q从C点同时出发,以相同的速度沿CA方向向A点匀速运动,当点P运动到B点时,P、Q两点同时停止运动,以PQ为边作正△PQM(P、Q、M按逆时针排序),以QC为边在AC上方作正△QCN,设点P运动时间为t秒.
(1)求cosA的值;
(2)当△PQM与△QCN的面积满足S△PQM=![]() S△QCN时,求t的值;
S△QCN时,求t的值;
(3)当t为何值时,△PQM的某个顶点(Q点除外)落在△QCN的边上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发负责送货,向东走了2千米到达小明家,继续向东走了4千米到达小红家,然后向西走了9千米到达小刚家,最后返回百货大楼.
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请你在数轴上标出小明、小红、小刚家的位置;
(2)小明家与小刚家相距多远?
(3)若货车每千米耗油0.5升,那么这辆货车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
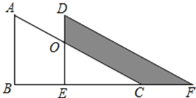
【题目】如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到![]() 的位置,AB=8,DO=2,平移距离为4,则阴影部分面积为( )
的位置,AB=8,DO=2,平移距离为4,则阴影部分面积为( )
A.28B.40C.42D.48
查看答案和解析>>
科目:初中数学 来源: 题型:
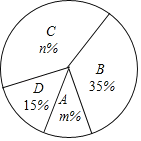
【题目】今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
等级 | 成绩(s) | 频数(人数) |
A | 90<s≤100 | 4 |
B | 80<s≤90 | x |
C | 70<s≤80 | 16 |
D | s≤70 | 6 |
根据以上信息,解答以下问题:
(1)表中的x= ;
(2)扇形统计图中m= ,n= ,C等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用a1,a2表示)和两名女生(用b1,b2表示),请用列表或画树状图的方法求恰好选取的是a1和b1的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的不断提高,人们对生活饮用水质量要求也越来越高,更多的居民选择购买家用净水器.一商家抓住商机,从生产厂家购进了![]() ,
,![]() 两种型号家用净水器.已知购进2台
两种型号家用净水器.已知购进2台![]() 型号家用净水器比1台
型号家用净水器比1台![]() 型号家用净水器多用200元;购进3台
型号家用净水器多用200元;购进3台![]() 型号净水器和2台
型号净水器和2台![]() 型号家用净水器共用6600元
型号家用净水器共用6600元
(1)求![]() ,
,![]() 两种型号家用净水器每台进价各为多少元?
两种型号家用净水器每台进价各为多少元?
(2)该商家用不超过26400元共购进![]() ,
,![]() 两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价
两种型号家用净水器20台,再将购进的两种型号家用净水器分别加价![]() 后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进
后出售,若两种型号家用净水器全部售出后毛利润不低于12000元,求商家购进![]() ,
,![]() 两种型号家用净水器各多少台?(注:毛利润
两种型号家用净水器各多少台?(注:毛利润![]() 售价
售价![]() 进价)
进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查.下面是根据收集的数据绘制的两幅不完整的统计图.
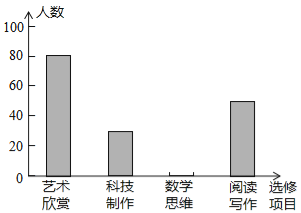
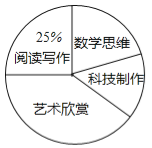
请根据图中提供的信息,解答下面的问题:
(1)此次共调查了 名学生,扇型统计图中“艺术鉴赏”部分的圆心角是 度.
(2)请把这个条形统计图补充完整.
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
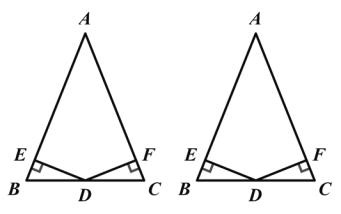
【题目】已知:如图,在△ABC 中,AB=AC,点 D 在 BC 上,DE⊥AB,DF⊥AC,垂足分别为点 E、F,且 DE=DF.
求证:点 D 为 BC 的中点.(请用两种不同的方法证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com