
分析 (1)根据题目信息列出算式,然后提取$\frac{1}{3}$,进行计算即可得解;
(2)观察不难发现,两个连续的自然数的积等于这两个数与后面的数的积减去与前面的数的积的$\frac{1}{3}$,然后列出算式进行计算即可得解;
(3)1×2+2×3+3×4根据(2)的规律列式进行计算,3×4×5+…+6×7×8可补上1×2×3+2×3×4,然后类比(2)中结论计算,再减去之前补上的1×2×3+2×3×4,总体列式计算可得;
(4)类比(3)中相同做法列式计算.
解答 解:(1)1×2+2×3+3×4+…+10×11,
=$\frac{1}{3}$×(1×2×3-0×1×2)+$\frac{1}{3}$×(2×3×4-1×2×3)+$\frac{1}{3}$×(3×4×5-2×3×4)+…+$\frac{1}{3}$×(6×7×8-5×6×7),
=$\frac{1}{3}$×(1×2×3-0×1×2+2×3×4-1×2×3+3×4×5-2×3×4+…+6×7×8-5×6×7),
=$\frac{1}{3}$×6×7×8,
=112;
(2)∵1×2+2×3+3×4=$\frac{1}{3}$×3×4×5,
∴1×2+2×3+3×4+…+n×(n+1)=$\frac{1}{3}$n(n+1)(n+2);
(3)1×2+2×3+3×4+3×4×5+…+6×7×8
=$\frac{1}{3}$×3×4×5+$\frac{1}{4}$×6×7×8×9-$\frac{1}{4}$×2×3×4×5
=20+756-30
=746;
(4)1×2+2×3+3×4+3×4×5+…+n×(n+1)×(n+2)
=$\frac{1}{3}$×3×4×5+$\frac{1}{4}$×n×(n+1)×(n+2)×(n+3)-$\frac{1}{4}$×2×3×4×5
=$\frac{1}{4}$n(n+1)(n+2)(n+3)-10.
点评 本题是对数字变化规律的考查,难度较大,利用类比的思想求解即可,观察出(2)的变化规律是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8-3+5-7 | B. | 3+8-7-5 | C. | -5-7-3+8 | D. | 8+3-5+7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
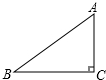 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.则sinB等于( )
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.则sinB等于( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com