
【题目】如图,在矩形 ABCD 中,AE 平分∠BAD,交 BC 于 E,过 E 做 EF⊥AD 于 F,连接BF交AE于P,连接PD.
(1)求证:四边形ABEF 是正方形;
(2)如果AB=6,AD=8,求tan∠ADP的值.
【答案】
(1)
证明:∵四边形ABCD是矩形,
∴∠FAB=∠ABE=90°,AF∥BE,
∵EF⊥AD,
∴∠FAB=∠ABE=∠AFE=90°,
∴四边形ABEF是矩形,
∵AE平分∠BAD,AF∥BE,
∴∠FAE=∠BAE=∠AEB,
∴AB=BE,
∴四边形ABEF是正方形.
(2)
解:过点P作PH⊥AD于H,如图所示:
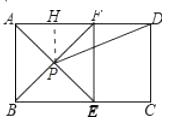
∵四边形ABEF是正方形,
∴BP=PF,BA⊥AD,∠PAF=45°,∴AB∥PH,
∵AB=6,∴AH=PH=3,
∵AD=8,∴DH=AD﹣AH=8﹣3=5,
在Rt△PHD中,∠PHD=90°.
∴tan∠ADP=![]() =
=![]()
【解析】(1)根据正方形的判定定理,先证明四边形ABEF是矩形,再证明邻相等可得其为正方形;
(2)求tan∠ADP需要构造直角三角形,所以过点P作PH⊥AD于H,从而可找到突破口.


科目:初中数学 来源: 题型:
【题目】如图,直线m,n的夹角为35°,相交于点O,
(1)作出△ABC关于直线m的对称△DEF;
(2)作出△DEF关于直线n的对称△PQR;
(3)△PQR还可以由△ABC经过一次怎样的变换得到.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).
与x轴交于点A和点B,与y轴交于点C,已知点B的坐标为(3,0).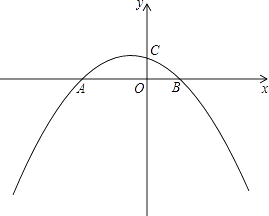
(1)求a的值和抛物线的顶点坐标;
(2)分别连接AC、BC.在x轴下方的抛物线上求一点M,使△AMC与△ABC的面积相等;
(3)设N是抛物线对称轴上的一个动点,d=|AN﹣CN|.探究:是否存在一点N,使d的值最大?若存在,请直接写出点N的坐标和d的最大值;若不存在,请简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学生社团为了解本校学生喜欢球类运动的情况,随机抽取了若干名学生进行问卷调查,要求每位学生只能填写一种自己喜欢的球类运动,并将调查的结果绘制成如下的两幅不完整的统计图. 
请根据统计图表提供的信息,解答下列问题:
(1)参加调查的人数共有人;在扇形图中,m=;将条形图补充完整;
(2)如果该校有3500名学生,则估计喜欢“篮球”的学生共有多少人?
(3)该社团计划从篮球、足球和乒乓球中,随机抽取两种球类组织比赛,请用树状图或列表法,求抽取到的两种球类恰好是“篮球”和“足球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD 中,AB=2,点E 在边AD 上,∠ABE=45°,BE=DE,连接BD,点P 在线段DE 上,过点P 作PQ∥BD 交BE 于点Q,连接QD.设PD=x,△PQD 的面积为y,则能表示y 与x 函数关系的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如 ![]() ,表示a1=a2+a3 , 则a1的最小值为( )
,表示a1=a2+a3 , 则a1的最小值为( ) 
A.32
B.36
C.38
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线MN上一点,OP⊥MN,在等腰Rt△ABO中,∠BAO=90°,AC∥OP交OM于C,D为OB的中点,DE⊥DC交MN于E.
(1)如图1,若点B在OP上,则
①ACOE(填“<”,“=”或“>”);
②线段CA、CO、CD满足的等量关系式是;
(2)将图1中的等腰Rt△ABO绕O点顺时针旋转α(0°<α<45°),如图2,那么(1)中的结论②是否成立?请说明理由;
(3)将图1中的等腰Rt△ABO绕O点顺时针旋转α(45°<α<90°),请你在图3中画出图形,并直接写出线段CA、CO、CD满足的等量关系式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,我国两艘海监船A,B在南海海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C,此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向,已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才能得到救援?(参考数据:sin53°≈ ![]() ,cos53°≈
,cos53°≈ ![]() ,tan53°≈
,tan53°≈ ![]() ,
, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】舟山市2010﹣2014年社会消费品零售总额及增速统计图如图: 
请根据图中信息,解答下列问题:
(1)求舟山市2010﹣2014年社会消费品零售总额增速这组数据的中位数.
(2)求舟山市2010﹣2014年社会消费品零售总额这组数据的平均数.
(3)用适当的方法预测舟山市2015年社会消费品零售总额(只要求列式说明,不必计算出结果).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com