
【题目】如图,已知AD为△ABC的高,AD=BC,以AB为底边作等腰Rt△ABE,EF∥AD,交AC于F,连ED,EC,有以下结论:①△ADE≌△BCE;②CE⊥AB;③BD=2EF;④S△BDE=S△ACE,其中正确的是( )

A.①②③B.②④C.①③D.①③④
【答案】D
【解析】
①易证∠CBE=∠DAE,即可求证:△ADE≌△BCE;
②根据①结论可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;
③证明△AEF≌△BED即可;
④易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.
如图延长CE交AD于K,交AB于H.设AD交BE于O.
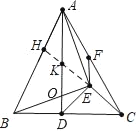
∵∠ODB=∠OEA,∠AOE=∠DOB,
∴∠OAE=∠OBD,
∵AE=BE,AD=BC,
∴△ADE≌△BCE,故①正确,
∴∠AED=∠BEC,DE=EC,
∴∠AEB=∠DEC=90°,
∴∠ECD=∠ABE=45°,
∵∠AHC=∠ABC+∠HCB=90°+∠EBC>90°,
∴EC不垂直AB,故②错误,
∵∠AEB=∠HED,
∴∠AEK=∠BED,
∵AE=BE,∠KAE=∠EBD,
∴△KAE≌△DBE,
∴BD=AK,
∵△DCK是等腰直角三角形,DE平分∠CDK,
∴EC=EK,
∵EF∥AK,
∴AF=FC,
∴AK=2EF,
∴BD=2EF,故③正确,
∵EK=EC,
∴S△AKE=S△AEC,
∵△KAE△DBE,
∴S△KAE=S△BDE,
∴S△BDE=S△AEC,故④正确.
故选:D.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,BO、CO是角平分线.
(1)∠ABC=50°,∠ACB=60°,求∠BOC的度数,并说明理由.
(2)题(1)中,如将“∠ABC=50°,∠ACB=60°”改为“∠A=70°”,求∠BOC的度数.
(3)若∠A=n°,求∠BOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,以AC为底边作等腰△ACD,且使∠ABC=2∠CAD,连接BD.

(1)如图1,若∠ADC=90°,∠BAC=30°,BC=1,求CD的长;
(2)如图1,若∠ADC=90°,证明:AB+BC=![]() BD;
BD;
(3)如图2,若∠ADC=60°,探究AB,BC,BD之间的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于任意两点A(x1,y1)B (x2,y2),规定运算:
(1)A⊕B=(x1+x2,y1+y2);
(2)A⊙B=x1x2+y1y2;
(3)当x1=x2且y1=y2时,A=B.
有下列四个命题:
①若有A(1,2),B(2,﹣1),则A⊕B=(3,1),A⊙B=0;
②若有A⊕B=B⊕C,则A=C;
③若有A⊙B=B⊙C,则A=C;
④(A⊕B)⊕C=A⊕(B⊕C)对任意点A、B、C均成立.
其中正确的命题为______(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
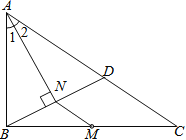
(1)求证:BN=DN;
(2)求△ABC的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从一副52张(没有大小王)的扑克中,每次抽出1张,然后放回洗匀再抽,在实验中得到下列表中部分数据:
实验次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
出现方块的次数 | 11 | 18 | a | 40 | 49 | 63 | 68 | 80 | 91 | 100 |
出现方块的频率 | 27.5% | 22.5% | 25% | 25% | 24.5% | 26.25% | 24.3% | b | 25% | 25% |
(1)填空a= ,b= ;
(2)从上面的图表中可以估计出现方块的概率是 ;
(3)将这幅扑克中的所有方块(即从方块1到方块13,共13张)取出,将它们背面朝上重新洗牌后,从中摸出一张,若摸出的这张牌面数字为奇数,则甲方贏,若摸出的这张牌的牌面数字是偶数,则乙方赢,你认为这个游戏对双方是公平的吗说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
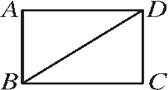
【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司购进10 000kg苹果,公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分结果如下表:
苹果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.50 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.105 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
估计这批苹果损坏的概率为_____(结果保留小数点后一位),损坏的苹果约有______kg.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件
B. 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
C. “明天降雨的概率为![]() ”,表示明天有半天都在降雨
”,表示明天有半天都在降雨
D. 了解一批电视机的使用寿命,适合用普查的方式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com