Question

11．如图，平面直角坐标系中，已知直线y=x上一点P（1，1），C为y轴上一点，连接PC，线段PC绕点P顺时针旋转90°至线段PD，过点D作直线AB⊥x轴，垂足为B；直线AB与直线y=x交于点A，连接CD，直线CD与直线y=x交于点Q．
（1）求证：OB=OC；
（2）当点C坐标为（0，3）时，求点Q的坐标；
（3）当△OPC≌△ADP时，直接写出C点的坐标．

Answer 1

分析 （1）作辅助线，构建全等三角形，证明CG=EB，证明四边形OGPE为正方形得OG=OE，所以OC=OB；
（2）先求点D的坐标，再利用待定系数法求直线CD的解析式，与直线OA的解析式列方程组求出点Q的坐标；
（3）设CG=x，根据△OPC≌△ADP表示出直角三角形APH各边的长，利用勾股定理列方程求出x的值，写出点C的坐标．

解答 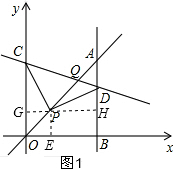证明：（1）过P作GH⊥OC，垂足为G，交AB于H，
过P作PE⊥x轴，垂足为E，
∵AB⊥OB，
∴GH⊥AB，
∵∠CPD=90°，
∴∠GPC+∠DPH=90°，
∠GCP+∠GPC=90°，
∴∠GCP=∠DPH，
又∵∠CGP=∠PHD=90°，PC=PD，
∴△CGP≌△PHD，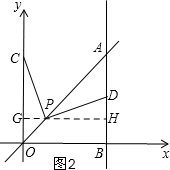
∴CG=PH，
∵∠PEB=∠EBH=∠BHP=90°，
∴四边形PEBH为矩形，
∴PH=EB，
∴CG=EB，
∵GH∥OB，OG∥PE，∠GOE=90°，
∴四边形GOEP为矩形，
∵直线OA：y=x，
∴∠GOP=∠POE=45°，
∵∠GPO=∠POE=45°，
∴∠GOP=∠GPO，
∴GO=GP，
∴矩形GOEP为正方形，
∴OG=OE，
∴OG+GC=OE+EB，
即OC=OB；
（2）∵P（1，1），
∴OG=BH=PG=DH=1，
∵C（0，3），
∴OB=OC=3，
∴D（3，2），
设直线CD的解析式为：y=kx+b，
把D（3，2）、C（0，3）代入得：$\left\{\begin{array}{l}{3k+b=2}\\{b=3}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=3}\end{array}\right.$，
∴直线CD的解析式为：y=-$\frac{1}{3}$x+3，
则$\left\{\begin{array}{l}{y=-\frac{1}{3}x+3}\\{y=x}\end{array}\right.$    解得$\left\{\begin{array}{l}{x=\frac{9}{4}}\\{y=\frac{9}{4}}\end{array}\right.$，
∴Q（$\frac{9}{4}$，$\frac{9}{4}$）；
（3）如图2，过P作GH⊥OC，垂足为G，交AB于H，
设CG=x，则PH=x，OC=x+1，
∵△OPC≌△ADP，
∴AP=OC=x+1，AD=OP=$\sqrt{2}$，
∴AH=$\sqrt{2}$+1，
在Rt△APH中，由勾股定理得：（x+1）²=x²+（$\sqrt{2}$+1）²，
x=$\sqrt{2}$+1，
∴C（0，2+$\sqrt{2}$）．

点评 本题是一次函数的综合题，综合考查了勾股定理、全等三角形、矩形、正方形等图形的性质及判定，知道旋转前后的两条线段的长相等，夹角等于旋转角；两直线的交点坐标可以利用解析式列方程组求解；本题还运用了勾股定理及三角形全等求线段的长．