
����Ŀ����ͼ����֪������y��ax2+bx������A(4��0)����B���䶥�㣬��AOB��45����OC��OB�����������ڵ�C����ֱ��y��kx�������߽��ڵ�D���ֱ����B��C��BE��CF��ֱ��ֱ��y��kx�ڵ�E��F��
(1)��������ߵĽ���ʽ��
(2)��ֱ��y��kx�ѡ�AOC�ֳɵ������ǵĶ���֮��ǡ��Ϊ1��2ʱ����k��ֵ��
(3)BE+CF�Ƿ�������ֵ�������ڣ���ֱ��д�������ֵ�ʹ�ʱk��ֵ���������ڣ���˵�����ɣ�

���𰸡�(1)y��![]() ��(2)k=
��(2)k=![]() ��k=2-
��k=2-![]() ��(3)���ڣ�BE+CF��4
��(3)���ڣ�BE+CF��4![]() ����ʱk=-2.
����ʱk=-2.
��������
(1)����B��BH��x���ڵ�H�������B�����꣬�ô���ϵ�������������ʽ��
(2)�������C�����꣬�������������ٵ���AOD��30��ʱ������D��DP��x���ڵ�P�������k��ֵ���ڵ���COD��30��ʱ����ͼ����CQ��OF�Ľ���ΪK������D��DP��x���ڵ�P������K��KN��OC��N��֤����ADP�ס�AKQ�����CN��CK��KQ�ij�����k��ֵ�������
(3)����BC���ɴ��߶���̿�֪BE+CF��BC�����ҽ���ֱ��y��kx��BC��ֱ������E��F�غ�ʱ��BE+CF��BC����ʱBE+CFȡ�����ֵ����������ֵ��k��ֵ��
�⣺(1)��A(4��0)��
��OA��4��
����B��BH��x���ڵ�H����ͼ1��
���OHB��90����OH��AH��2��
�ߡ�AOB��45����
���OBH����AOB��45����
��OH��BH��2��
���B������Ϊ(2����2)��
��![]() ��
��
��ã� ��
��
��������ߵĽ���ʽΪy��![]() ��
��

(2)��ͼ2������C��CQ��x���ڵ�Q��
��OC��OB����AOB��45����
���COA����AOB��45����
��CQ��OQ��
��![]() =x����ã�x1��0��x2��6��
=x����ã�x1��0��x2��6��
���C������Ϊ(6��6)��
��ֱ��y��kx�ѡ�AOC�ֳɵ������ǵĶ���֮��ǡ��Ϊ1��2��
��ٵ���AOD��30��ʱ������D��DP��x���ڵ�P��
k��![]() =tan30��=
=tan30��=![]() ��
��

�ڵ���COD��30��ʱ����ͼ3����CQ��OF�Ľ���ΪK������D��DP��x���ڵ�P������K��KN��OC��N��
��DP��CQ����CNK����ONK��90����
��![]() ��
��
��k��![]() ��
��
�֡ߡ�OCQ��45����
��CN��KN��CK��![]() ��
��
��OC��ON+NC��(![]() +1)CN��
+1)CN��
�ߡ�BOC��90������B��C������ֱ�Ϊ(2����2)��(6��6)��COF����AOB��45����
��OB��![]() ��OC��
��OC��![]() ��
��
��![]() ��
��
��CN��3![]() ��
��
��![]() ��
��![]()
��KQ��CQ��CK��6��(6![]() -6)��12��6
-6)��12��6![]() ��
��
��k��![]() =
=![]() =2-
=2-![]() ��
��

(3)��ͼ4������BC���ɴ��߶���̿�֪BE+CF��BC��
���ҽ���ֱ��y��kx��BC��ֱ������E��F�غ�ʱ��BE+CF��BC����ʱBE+CFȡ�����ֵ��

��BE+CF��![]() =4
=4![]() ��
��
D�������Ϊ(3����1.5)��
k����2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ֱ�����ǰ���һ�麬30����ֱ�����ǰ���һ�����ֱ�����ǰ���ɣ��Һ�30���ǵ����ǰ�Ľϳ�ֱ�DZ�����һ���ǰ��б����ȣ���ͼ1��

��1����ͼ1���⸱���ǰ��У���֪AB��2��AC���� ����A��D���� ��
��2���⸱���ǰ���ͼ1���ã�����A��DC���̶�����������ABCͨ����ת����ƽ�Ʊ任��ʹ��ABC��б��BC������A��DC�����ֱ�Ƕ���D��
����һ����ͼ2������ABC�Ƶ�C��˳ʱ�뷽����ת�Ƕ�����0��������180����
����������ͼ3������ABC������A��C������ƽ��m����λ����
����������ͼ4������ABC�Ƶ�A����ʱ�뷽����ת�Ƕ�����0��������180����
�������������⣺
�ٸ��ݷ���һ��ֱ��д������ֵΪ���� ����
�ڸ��ݷ�����������m��ֵ��
�۸��ݷ�������������ֵ��
��3��������ABC��ͼ1λ�ÿ�ʼ������A��C��ƽ�ƣ���AA����x�����������ص����ֵ����Ϊy����ֱ��д��y��x֮��ĺ�����ϵʽ����Ӧ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
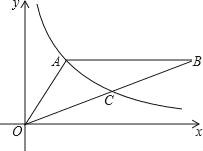
����Ŀ����ͼ��˫����y��![]() ��x��0��������OAB�Ķ���A��OB���е�C��AB��x�ᣬ��A������Ϊ��2��3�������OAB�����_____��
��x��0��������OAB�Ķ���A��OB���е�C��AB��x�ᣬ��A������Ϊ��2��3�������OAB�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A![]() ��B��-1,2����һ�κ���
��B��-1,2����һ�κ���![]() �뷴��������
�뷴��������![]()
��![]() ��ͼ����������㣬AC��x����C��BD��y����D��
��ͼ����������㣬AC��x����C��BD��y����D��
(1)����ͼ��ֱ�ӻش��ڵڶ������ڣ���xȡ��ֵʱ��һ�κ������ڷ�����������ֵ?
(2)��һ�κ�������ʽ��m��ֵ��
(3)P���߶�AB�ϵ�һ�㣬����PC��PD������PCA����PDB�����ȣ����P���꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Rt��ABC��ֱ�Ƕ���B��y���ϣ���AB��x���ڵ�D(![]() ��0)����C������Ϊ(��4��0)������������y��
��0)����C������Ϊ(��4��0)������������y��![]() (k��0)��ͼ�����A����k��_____��
(k��0)��ͼ�����A����k��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪʹ��һ������У��ʱ���Ϻ�����У��������ǰ��ijУ���꼶����ѧ����������У���ͺ���������������飬�����ݵ�������������ͼ������������ͳ��ͼ��У���ͺ���������Ϊ��������Ϊ6���ͺţ���
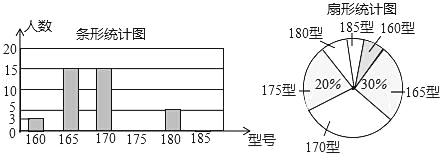
����������Ϣ������������⣺
��1���ð���� ����ѧ����
��2����ȫ����ͳ��ͼ��
��3���ð�ѧ������У���ͺŵ�����Ϊ�� ������λ��Ϊ�� ����
��4�������УԤ����������1500���������������ݣ�����������170��У����ѧ����Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
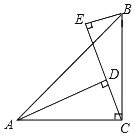
����Ŀ����֪����ͼ����ACB��90����AC��BC��AD��CE��BE��CE������ֱ��ǵ�D��E��
��1����֤����BEC�ա�CDA��
��2����AD��3��BE��1ʱ����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��![]() x+a��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��������y��
x+a��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��������y��![]() x2+bx+c������A��B����M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ�߷ֱ�ֱ��AB���������ڵ�P��N��
x2+bx+c������A��B����M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ�߷ֱ�ֱ��AB���������ڵ�P��N��
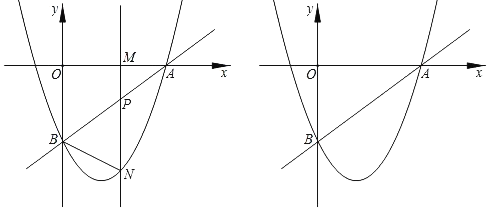
��1����գ���B������Ϊ�� ���������ߵĽ���ʽΪ�� ����
��2������M���߶�OA���˶�ʱ�������O��A�غϣ���
�ٵ�mΪ��ֵʱ���߶�PN���ֵ�������PN�����ֵ�������ʹ��BPNΪֱ��������ʱm��ֵ��
��3����������������ֻ��������N��ֱ��AB�ľ�����h����ֱ��д����ʱ�ɵ�O��B��N��P���ɵ��ı��ε������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ߳�Ϊ1����λ���ȵ������������н�����ͼ��ʾ��ƽ��ֱ������ϵ����ABC�Ķ��㶼�ڸ���ϣ������������⣺

��1����������ABC����ƽ��4����λ���Ⱥ�õ�����A1B1C1�� ��д����C1�����ꣻ
��������ABC����ԭ��O�ԳƵ���A2B2C2�� ��д����C2�����ꣻ
��2����֪��ABC����ֱ��l�ԳƵ���A3B3C3�Ķ���A3������Ϊ����4����2������ֱ��д��ֱ��l�ĺ�������ʽ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com