
����Ŀ����ͼ��ֱ��y��![]() x+a��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��������y��
x+a��x�ύ�ڵ�A��4��0������y�ύ�ڵ�B��������y��![]() x2+bx+c������A��B����M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ�߷ֱ�ֱ��AB���������ڵ�P��N��
x2+bx+c������A��B����M��m��0��Ϊx����һ���㣬����M�Ҵ�ֱ��x���ֱ�߷ֱ�ֱ��AB���������ڵ�P��N��
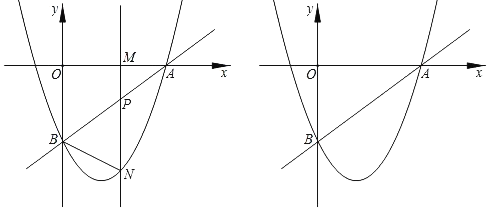
��1����գ���B������Ϊ�� ���������ߵĽ���ʽΪ�� ����
��2������M���߶�OA���˶�ʱ�������O��A�غϣ���
�ٵ�mΪ��ֵʱ���߶�PN���ֵ�������PN�����ֵ�������ʹ��BPNΪֱ��������ʱm��ֵ��
��3����������������ֻ��������N��ֱ��AB�ľ�����h����ֱ��д����ʱ�ɵ�O��B��N��P���ɵ��ı��ε������
���𰸡���1����0����3����y��![]() x2��
x2��![]() x��3����2������3����3��
x��3����2������3����3��![]() ����3��6��6+6
����3��6��6+6![]() ��6
��6![]() ��6��
��6��
��������
(1)�ѵ�A���������ֱ�߱���ʽy��![]() x+a�����a=-3���ѵ�A��B�����������κ�������ʽ��������ֵ.
x+a�����a=-3���ѵ�A��B�����������κ�������ʽ��������ֵ.
(2) �ٵ�P��m��![]() m��3������N��m��
m��3������N��m��![]() m2��
m2��![]() m��3�����PNֵ�ı���ʽ��������⣬
m��3�����PNֵ�ı���ʽ��������⣬
�ڷ֡�BNP��90������NBP��90������BPN��90������������ֱ����.
(3)����������ֻ��������N��ֱ��AD�ľ�����h,��ֻ�ܳ��֣���ABֱ���·������������N��ֱ������������һ������N����ֱ��AB�Ϸ��Ľ������������ֱ���⼴��.
�⣺��1���ѵ�A�������ֱ�߱���ʽy��![]() x+a��
x+a��
��ã�a����3����ֱ�߱���ʽΪ��y�T![]() x��3����x��0����y����3��
x��3����x��0����y����3��
���B������0����3����
����B�����������κ�������ʽ�ã�c����3��
�ѵ�A�����������κ�������ʽ�ã�![]() ��16+4b��3��0��
��16+4b��3��0��
��ã�b����![]() ��
��
�������ߵĽ���ʽΪ��y��![]() x2��
x2��![]() x��3��
x��3��
��2���١�M��m��0�����߶�OA�ϣ���MN��x�ᣬ
���P��m��![]() m��3����N��m��
m��3����N��m��![]() m2��
m2��![]() m��3����
m��3����
��PN��![]() m��3����
m��3����![]() m2��
m2��![]() m��3������
m��3������![]() ��m��2��2+3��
��m��2��2+3��
��a����![]() ��0��
��0��
�������߿������£�
�൱m��2ʱ��PN�����ֵ��3��
�ڵ���BNP��90��ʱ����N��������Ϊ��3��
��y����3���������ߵı���ʽ�ã���3��![]() m2��
m2��![]() m��3����ã�m��3��0����ȥm��0����
m��3����ã�m��3��0����ȥm��0����
��m��3��
����NBP��90��ʱ����BN��AB����ֱ�ߴ�ֱ����kֵ���Ϊ��1��
�裺ֱ��BN�ı���ʽΪ��y����![]() x+n��
x+n��
�ѵ�B�����������ʽ����ã�n����3����ֱ��BN�ı���ʽΪ��y����![]() x��3��
x��3��
����ʽ�������ߵı���ʽ��������ã�m��![]() ��0����ȥm��0����
��0����ȥm��0����
����BPN��90��ʱ������������ȥ��
�ʣ�ʹ��BPNΪֱ��������ʱm��ֵΪ3��![]() ��
��
��3����OA��4��OB��3��
��Rt��AOB��tan����![]() ����cos����
����cos����![]() ��sin����
��sin����![]() ��
��
��PM��y�ᣬ
���BPN����ABO������

��������������ֻ��������N��ֱ��AB�ľ�����h��
��ֻ�ܳ��֣���ABֱ���·������������N��ֱ������������һ������N����ֱ��AB�Ϸ��Ľ�����������
������N��ֱ������������һ������N��
��M������Ϊ��m��0�����裺��N����Ϊ����m��n����
��n��![]() m2��
m2��![]() m��3������N��AB��ƽ���ߣ�
m��3������N��AB��ƽ���ߣ�
���N���ڵ�ֱ�߱���ʽΪ��y��![]() x+b������N������룬
x+b������N������룬
��ã���N��ֱ�߱���ʽΪ��y��![]() x+��n��
x+��n��![]() m����
m����
�������ߵı���ʽ����ʽ�����������ã�3x2��12x��12+3m��4n��0��
����144��3��4������12+3m��4n����0��
��n��![]() m2��
m2��![]() m��3������ʽ�������ã�m2��4m+4��0��
m��3������ʽ�������ã�m2��4m+4��0��
��ã�m��2�����N������Ϊ��2����![]() ����
����
��P������2����![]() ����
����
��PN��3��
��OB��3��PN��OB��
���ı���OBNPΪƽ���ı��Σ����O��ֱ��AB�ľ�����ڵ�N��ֱ��AB�ľ��룬
��������O��ABƽ�е�ֱ���������ߵĽ���Ϊ��������N�㣬����N����N����
ֱ��ON�ı���ʽΪ��y��![]() x�����ñ���ʽ����κ�������ʽ�����������ã�
x�����ñ���ʽ����κ�������ʽ�����������ã�
x2��4x��4��0����ã�x��2��2![]() ��
��
���N����N���ĺ�����ֱ�Ϊ2+2![]() ��2��2
��2��2![]() ��
��
��NH��AB��ֱ��AB�ڵ�H��
��h��NH��NPsin����![]() ��
��
��N��P����x�ᣬ��x���ڵ�P������ON��P��������ON����![]() ��
��![]() ��2+2
��2+2![]() ����
����
S�ı���OBPN��BPh��![]() ��6��
��6��
��S�ı���OBP��N����S��OP��N��+S��OBP����6+![]() ��
��
ͬ����S�ı���OBN��P����![]() ��6��
��6��
�ʣ���O��B��N��P���ɵ��ı��ε����Ϊ��6��6+6![]() ��6
��6![]() ��6��
��6��


 �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д� Сѧ�̲���ȫ���ϵ�д�
Сѧ�̲���ȫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
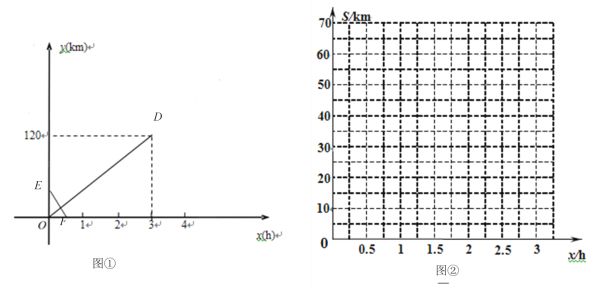
����Ŀ����֪A��C��B����������һ��ֱ���ϣ�����Ħ�г�ֱ�Ӵ�C��ǰ��B�أ��ҿ�����80km/h���ٶȴ�A��ǰ��B�أ���C�ذ���������1 h����ǰ��B�أ���֪����ͬʱ�������ٶȲ��䣬��ǡ��ͬʱ����B�أ������x h�����������C�صľ���ֱ�Ϊy1 kmy2 km��ͼ�����߶�OD��ʾy1��x�ĺ���ͼ���߶�EF��ʾy2��x�����IJ���ͼ��
��1�����ٶ�Ϊ km/h����E����Ϊ ��
��2�����߶�EF����ʾ��y2��x֮��ĺ�������ʽ��
��3�����������Sǧ�ף���ͼ��������ֱ������ϵ�л���S����x�ĺ���ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������y��ax2+bx������A(4��0)����B���䶥�㣬��AOB��45����OC��OB�����������ڵ�C����ֱ��y��kx�������߽��ڵ�D���ֱ����B��C��BE��CF��ֱ��ֱ��y��kx�ڵ�E��F��
(1)��������ߵĽ���ʽ��
(2)��ֱ��y��kx�ѡ�AOC�ֳɵ������ǵĶ���֮��ǡ��Ϊ1��2ʱ����k��ֵ��
(3)BE+CF�Ƿ�������ֵ�������ڣ���ֱ��д�������ֵ�ʹ�ʱk��ֵ���������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�ڣ�С����������ı߳�Ϊ1����λ���ȣ���ABC���������������ֱ�ΪA����1��3����B����4��0����C����0��0��
��1������ABC����ƽ��1����λ���ȣ�������ƽ��5����λ���Ⱥ�õ�����A1B1C1��������A1B1C1����ֱ��д����A1�����ꣻ
��2����ABC��ԭ��O��ʱ�뷽����ת90���õ���A2B2O��
��3�������A2B2O��ͨ����ת���Եõ���A1B1C1����ֱ��д����ת����P������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���֪��A����3��0����B��0��4�����ԡ�OAB��������ת�任�����εõ���1����2����3����4���������2019��ֱ�Ƕ��������Ϊ��������

A. ��8076��0��B. ��8064��0��C. ��8076��![]() ��D. ��8064��
��D. ��8064��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AC�Ǿ���ABCD��һ���Խ��ߣ�E��AC�е㣬����BE���ٷֱ���A��DΪԲ�ģ�����![]() �ij�Ϊ�뾶�����������ཻ�ڵ�F������EF��AD�ڵ�G����AB��3��BC��4�����ı���ABEG���ܳ�Ϊ( )
�ij�Ϊ�뾶�����������ཻ�ڵ�F������EF��AD�ڵ�G����AB��3��BC��4�����ı���ABEG���ܳ�Ϊ( )
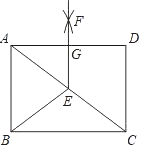
A. 8B. 8.5C. 9D. 9.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��B�Ƿ���������y��![]() ��k��0��x��0��ͼ���ϵ����㣬BC��x�ᣬ��y���ڵ�C������P������ԭ��O��������O��A��B��C��ͼ����������ʾ·�ߣ������˶����յ�ΪC����P��PM��x�ᣬ����ΪM����������OMP�����ΪS��P���˶�ʱ��Ϊr����S����t�ĺ���ͼ�����Ϊ��������
��k��0��x��0��ͼ���ϵ����㣬BC��x�ᣬ��y���ڵ�C������P������ԭ��O��������O��A��B��C��ͼ����������ʾ·�ߣ������˶����յ�ΪC����P��PM��x�ᣬ����ΪM����������OMP�����ΪS��P���˶�ʱ��Ϊr����S����t�ĺ���ͼ�����Ϊ��������

A. 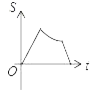 B.
B. 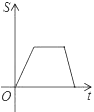 C.
C. 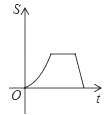 D.
D. 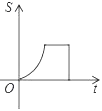
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ���Բ�����̳����˽������ij��ѧ�����ȡ�˲���ѧ�������ʾ����飬��������������![]() �dz��˽⣬
�dz��˽⣬![]() �˽⣬
�˽⣬![]() �˽���٣�
�˽���٣�![]() ���˽⣮������ֱ�ͳ�ƣ�����������������ͳ��ͼ(������)�������ͼ����Ϣ������������⣺
���˽⣮������ֱ�ͳ�ƣ�����������������ͳ��ͼ(������)�������ͼ����Ϣ������������⣺
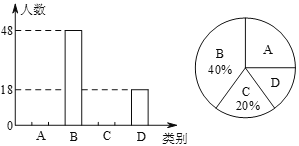
(1)�˴ι�������______��ѧ��������ͳ��ͼ��![]() ���ڵ����ε�Բ�ĽǶ���Ϊ______��
���ڵ����ε�Բ�ĽǶ���Ϊ______��
(2)������ͳ��ͼ����������
(3)����У����1600��ѧ����������ƶԲ�����̳����˽����Ϊ���dz��˽�����ѧ��Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�OA��3��OC��2����F��AB�ϵ�һ�����㣨F����A��B�غϣ�������F�ķ���������y��![]() ��ͼ����BC�߽��ڵ�E��
��ͼ����BC�߽��ڵ�E��
��1����FΪAB���е�ʱ����ú����Ľ���ʽ��
��2����kΪ��ֵʱ����EFA���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com