
分析 (1)先根据分式混合运算的法则把原式进行化简,再把a的值代入进行计算即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x=3y代入进行计算即可.
解答 解:(1)原式=$\frac{1}{a-1}$+$\frac{a+1}{a-1}$
=$\frac{a+2}{a-1}$,
当a=$\frac{1}{10}$时,原式=$\frac{\frac{1}{10}+2}{\frac{1}{10}-1}$=-$\frac{21}{9}$;
(2)原式=$\frac{4xy}{(x+y)(x-y)}$-$\frac{(x+y)^{2}}{(x-y)(x+y)}$
=$\frac{4xy-(x+y)^{2}}{(x+y)(x-y)}$,
当x=3y时,原式=$\frac{4y•3y-{(3y+y)}^{2}}{(3y+y)(3y-y)}$=$\frac{12{y}^{2}-16{y}^{2}}{8{y}^{2}}$=$\frac{-4{y}^{2}}{8{y}^{2}}$=-$\frac{1}{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:选择题
 如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:| A. | 两人皆正确 | B. | 两人皆错误 | C. | 甲正确,乙错误 | D. | 甲错误,乙正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
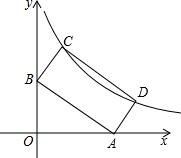 如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.
如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com