
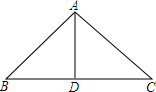
 如图,一只蜘蛛在等腰Rt△ABC钢梁上织网纲,∠BAC=90°,AB=AC=8,E在AB上,BE=2,要在顶梁柱AD(中线)上定一点F,从B点到F点拉网纲,再从F点到E点拉网纲.
如图,一只蜘蛛在等腰Rt△ABC钢梁上织网纲,∠BAC=90°,AB=AC=8,E在AB上,BE=2,要在顶梁柱AD(中线)上定一点F,从B点到F点拉网纲,再从F点到E点拉网纲.分析 (1)利用轴对称求最短路径得出F点位置,进而利用三角形三边关系得出答案;
(2)利用等腰直角三角形的性质结合勾股定理的出答案;
(3)利用(2)中解题思路,结合勾股定理求出答案.
解答 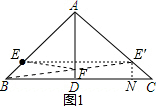 解:(1)如图1:作E点关于直线AD的对称点E′,连接BE′,交AD于点F,
解:(1)如图1:作E点关于直线AD的对称点E′,连接BE′,交AD于点F,
F点即为所求,
证明:由对称的性质可得:EF=FE′,此时BE′在一条直线上,在AD上任取一点与B,E′构成三角形,利用三角形两边之和大于第三边可得BE′最小,即可得出,BF+FE最短;
(2)如图1,过点E′,作E′N⊥BC于点N,
∵∠BAC=90°,AB=AC=8,
∴BC=8$\sqrt{2}$,
∵BE=2,则CE′=2,
∴E′C=NC=$\sqrt{2}$,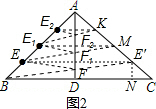 ∴BN=7$\sqrt{2}$,
∴BN=7$\sqrt{2}$,
在△BNE′中,BE′=$\sqrt{(7\sqrt{2})^{2}+(\sqrt{2})^{2}}$=10;
(3)如图2,由(2)可得:BF+EF=10,
同理可得:EF1+E1F1=EM=$\sqrt{52}$=2$\sqrt{13}$,E1K=E1F2+E2F2=$\sqrt{20}$=2$\sqrt{5}$,
故这些网纲之和最短时的长度和为:10+2$\sqrt{13}$+2$\sqrt{5}$.
点评 此题主要考查了利用轴对称取最短路线以及勾股定理,正确利用轴对称求出F点位置是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
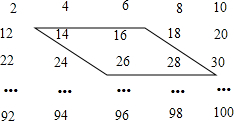 下列数阵是由50个偶数排成的.
下列数阵是由50个偶数排成的.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售出件数 | 7 | 6 | 7 | 8 | 2 |
| 售价(元) | +5 | +1 | 0 | -2 | -5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com