
【题目】如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=![]() (∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
(∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
其中正确的是( )

A.①②③B.①③④C.①②③④D.①②④
【答案】C
【解析】
①根据BD⊥FD,FH⊥BE和∠FGD=∠BGH,证明结论正确;
②根据角平分线的定义和三角形外角的性质,证明结论正确;
③证明∠DBE=∠BAC-∠C,根据①的结论,证明结论正确;
④根据角平分线的定义和三角形外角的性质证明结论正确.
①∵BD⊥FD,
∴∠FGD+∠F=90°,
∵FH⊥BE,
∴∠BGH+∠DBE=90°,
∵∠FGD=∠BGH,
∴∠DBE=∠F,
①正确;
②∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,
②正确;
③∠ABD=90°-∠BAC,
∠DBE=∠ABE-∠ABD=∠ABE-90°+∠BAC=∠CBD-∠DBE-90°+∠BAC,
∵∠CBD=90°-∠C,
∴∠DBE=∠BAC-∠C-∠DBE,
由①得,∠DBE=∠F,
∴∠F=∠BAC-∠C-∠DBE,
∴∠F=![]() (∠BAC﹣∠C)
(∠BAC﹣∠C)
③正确;
④∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=∠FEB,
∴∠BGH=∠ABE+∠C,
④正确,
故选C.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,M、N分别是边OA、OB上的定点,P、Q分别是边OB、OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1、∠2的数量关系正确的是( )

A.∠1+∠2=90°B.2∠2-∠1=30°
C.2∠1+∠2=180°D.∠1-∠2=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程mx2-2x+1=0.
(1)若方程有两个实数根,求m的取值范围;
(2)若方程的两个实数根为x1,x2,且x1x2-x1-x2=![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在△ABC中,∠B=2∠C,点D为线段BC上一动点,当AD满足某种条件时,探讨在线段AB、BD、CD、AC四条线段中,某两条或某三条线段之间存在的数量关系.
例如:在图1中,当AB=AD时,可证得AB=DC,现在继续探索:
任务要求:
(1)当AD⊥BC时,如图2,求证:AB+BD=DC;
(2)当AD是∠BAC的角平分线时,判断AB、BD、AC的数量关系,并证明你的结论。
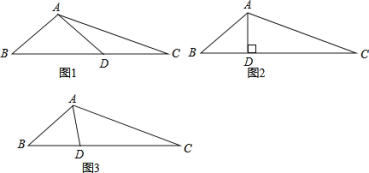
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,P是抛物线y=-x2+3x上一点,且在x轴上方,过点P分别向x轴、y轴作垂线,得到矩形PMON.若矩形PMON的周长随点P的横坐标m增大而增大,则m的取值范围是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx-3a经过A(-1,0),C(0,-3)两点,与x轴交于另一点B.
(1)求此抛物线的表达式;
(2)已知点D(m,-m-1)在第四象限的抛物线上,求点D关于直线BC对称的点D′的坐标;
(3)在(2)的条件下,连接BD.问在x轴上是否存在点P,使∠PCB=∠CBD?若存在,请求出P点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人400元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按七折收费;乙旅行社的优惠条件是:家长、学生都按八折收费假设这两位家长带领x名学生去旅游.
(1)如果设选择甲旅行社所用的费用为![]() 元,选择乙旅行社所用的费用为
元,选择乙旅行社所用的费用为![]() 元.请写出
元.请写出![]() 、
、![]() 与x的关系式.
与x的关系式.
(2)在(1)的前提下,请你帮助两位家长根据所带学生人数,选择哪家旅行社合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com