
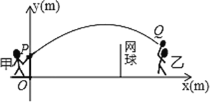
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分. 如图,甲在O点正上方1 m的点P发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数表达式:![]() ,已知点O与球网的水平距离为5 m,球网的高度1.55 m.
,已知点O与球网的水平距离为5 m,球网的高度1.55 m.
(1)当![]() 时,求h的值,并通过计算判断此球能否过网;
时,求h的值,并通过计算判断此球能否过网;
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7m,离地面的高度为![]() 的Q处时,乙扣球成功,求a的值.
的Q处时,乙扣球成功,求a的值.
科目:初中数学 来源: 题型:
【题目】如图,坡AB的坡比为1:2.4,坡长AB=130米,坡AB的高为BT.在坡AB的正面有一栋建筑物CH,点H、A、T在同一条地平线MN上.

(1)试问坡AB的高BT为多少米?
(2)若某人在坡AB的坡脚A处和中点D处,观测到建筑物顶部C处的仰角分别为60°和30°,试求建筑物的高度CH.(精确到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(问题发现)
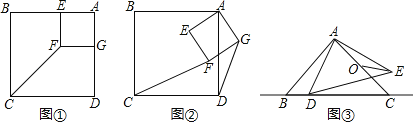
如图①,正方形AEFG的两边分别在正方形ABCD的边AB和AD上,连接CF.
填空:①线段CF与DG的数量关系为 ;
②直线CF与DG所夹锐角的度数为 .
(2)(拓展探究)
如图②,将正方形AEFG绕点A逆时针旋转,在旋转的过程中,(1)中的结论是否仍然成立,请利用图②进行说明.
(3(解决问题)
如图③,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O为AC的中点.若点D在直线BC上运动,连接OE,则在点D的运动过程中,线段OE长的最小值为 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
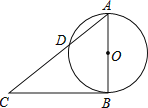
【题目】如图,AB是⊙O的直径,点C是⊙O外的一点,CB与⊙O相切于点B,AC交⊙O于点D,点E是![]() 上的一点(不与点A,B,D重合),若∠C=48°,则∠AED的度数为_____.
上的一点(不与点A,B,D重合),若∠C=48°,则∠AED的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
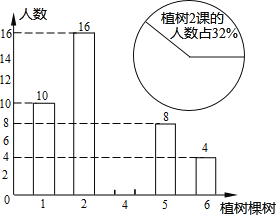
【题目】今年3月12日,某校九年级部分学生参加植树节活动,参加植树生植树情况的部分统计结果如图所示.请根据统计图形所提供的有关信息,完成下问题:
(1)求参加植树的学生人数;
(2)求参加学生植树棵树的平均数;(精确到1)
(3)请将该条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤![]() .其中正确结论的是( )
.其中正确结论的是( )
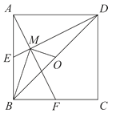
A. ①③④B. ②④⑤C. ①③⑤D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA
与⊙O的另一个交点为E,连结AC,CE。

(1)求证:∠B=∠D;
(2)若AB=4,BC-AC=2,求CE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,点
,点![]() 分别是直线
分别是直线![]() 与抛物线上的点,若点
与抛物线上的点,若点![]() 围成的四边形是平行四边形,则点
围成的四边形是平行四边形,则点![]() 的坐标为__________.
的坐标为__________.
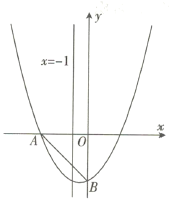
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣![]() x+6与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
x+6与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
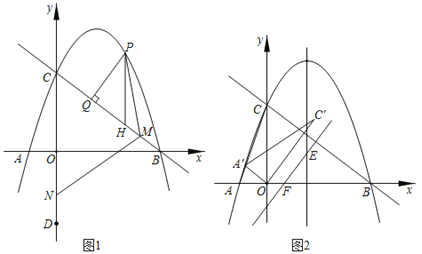
(1)如图1,点P为直线BC上方抛物线上一动点,过点P作PH∥y轴,交直线BC于点H,过点P作PQ⊥BC于点Q,当PQ﹣![]() PH最大时,点C关于x轴的对称点为点D,点M为直线BC上一动点,点N为y轴上一动点,连接PM、MN,求PM+MN+
PH最大时,点C关于x轴的对称点为点D,点M为直线BC上一动点,点N为y轴上一动点,连接PM、MN,求PM+MN+![]() ND的最小值;
ND的最小值;
(2)如图2,连接AC,将△OAC绕着点O顺时针旋转,记旋转过程中的△OAC为△OA'C',点A的对应点为点A',点C的对应点为点C'.当点A'刚好落在线段AC上时,将△OA'C'沿着直线BC平移,在平移过程中,直线OC'与抛物线对称轴交于点E,与x轴交于点F,设点R是平面内任意一点,是否存在点R,使得以B、E、F、R为顶点的四边形是菱形?若存在,请直接写出点R的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com