
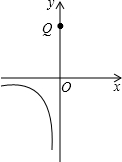
 ����ƽ��ֱ������ϵxOy�еĵ�P��a��b��������P�������Ϊ��a+$\frac{b}{k}$��ka+b��������kΪ��������k��0������Ƶ�P��Ϊ��P�ġ�k�������㡱�����磺P��2��4���ġ�2�������㡱ΪP�䣨2+$\frac{4}{2}$��2��2+4������P�䣨4��8����
����ƽ��ֱ������ϵxOy�еĵ�P��a��b��������P�������Ϊ��a+$\frac{b}{k}$��ka+b��������kΪ��������k��0������Ƶ�P��Ϊ��P�ġ�k�������㡱�����磺P��2��4���ġ�2�������㡱ΪP�䣨2+$\frac{4}{2}$��2��2+4������P�䣨4��8�������� ��1����ֻ���a=2��b=-1��k=2���루a+$\frac{b}{k}$��ka+b���������P������꣮
����P�䣨-2��-2�������k=1���Ӷ���a+b=-2����ȡһ��a�Ϳ������Ӧ��b���Ӷ��õ����������ĵ�P��һ�����꣮
��2�����P����Ϊ��a��0�����Ӷ���P�䣨a��ka������ȻPP���OP���������ɵ�OP=PP�䣬�Ӷ����k��
��3�����B������Ϊ��m��n�����Ӷ���ʾ����A�����꣨m+$\frac{n}{\sqrt{3}}$��$\sqrt{3}$m+n������A�ں���y=$\frac{\sqrt{3}}{x}$��x��0����ͼ���ϣ���B������Ϊ��m��-$\sqrt{3}$m-$\sqrt{3}$����Ȼ��BQ2��m�Ĵ���ʽ��ʾ�����ݶ��κ�������ֵ�ԣ����BQ��Сʱ��Ӧ��m��ֵ���Ӷ������Ӧ�ĵ�B�����꣮
��� �⣺��1���ٵ�a=-1��b=-2��k=2ʱ��
a+$\frac{b}{k}$=-1+$\frac{-2}{2}$=-2��ka+b=2����-1��-2=-4��
���P��-1��-2���ġ�2�������㡱P�������Ϊ��-2��-4����
�ʴ�Ϊ����-2��-4����
��������ã�$\left\{\begin{array}{l}{a+\frac{b}{k}=-2}\\{ka+b=-2}\end{array}\right.$��
��ã�k=1��
��a+b=-2��
��b=-2-a��
��a=1ʱ��b=-3����ʱ��P������Ϊ��1��-3����
�ʴ�Ϊ����1��-3����
��2���ߵ�P��x����������ϣ�
��b=0��a��0��
���P��������a��0������P���������a��ka����
��PP���OP��
�ߡ�OPP��Ϊ����ֱ�������Σ�
��OP=PP�䣮
��a=��ka��
��a��0��
��k=��1��
�ʴ�Ϊ����1��
��3�����B��������m��n����
�ߵ�A�ǵ�B�ġ�$\sqrt{3}$�������㡱��
���A��������m+$\frac{n}{\sqrt{3}}$��$\sqrt{3}$m+n����
�ߵ�A�ں���y=$\frac{\sqrt{3}}{x}$��x��0����ͼ���ϣ�
�ࣨm+$\frac{n}{\sqrt{3}}$ ����$\sqrt{3}$m+n��=$\sqrt{3}$����m+$\frac{n}{\sqrt{3}}$��0��
�������$\sqrt{3}$m+n��2=3��
��m+$\frac{n}{\sqrt{3}}$��0��
��$\sqrt{3}$m+n=-$\sqrt{3}$��
��n=-$\sqrt{3}$m-$\sqrt{3}$��
���B��������m��-$\sqrt{3}$m-$\sqrt{3}$����
����B��BH��OQ������ΪH����ͼ��ʾ��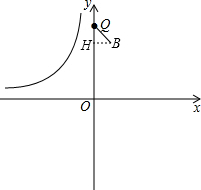
�ߵ�Q������Ϊ��0��2$\sqrt{3}$����
��QH2=��-$\sqrt{3}$m$-\sqrt{3}$-2$\sqrt{3}$��2=��$\sqrt{3}$m+3$\sqrt{3}$��2��BH2=m2��
��BQ2=BH2+QH2=m2+��$\sqrt{3}$m+3$\sqrt{3}$��2=4m2+18m+27=4��m+$\frac{9}{4}$��2+$\frac{27}{4}$��
��4��0��
�൱m=-$\frac{9}{4}$ʱ��BQ2��С����BQ��С��
��ʱn=-$\sqrt{3}$m-$\sqrt{3}$=$\frac{5\sqrt{3}}{4}$��
�൱�߶�BQ���ʱ��B������Ϊ��-$\frac{9}{4}$��$\frac{5\sqrt{3}}{4}$����
���� ���⿼���˷�����ͼ���ϵ����������������ֱ�������Ρ����κ�������ֵ������ϵ������֪ʶ���������¶����µ��Ķ�������������һ�����ۺ��ԣ��ڣ�2��������OP=PP��õ�a��ka֮��Ĺ�ϵ�DZ�����״��㣬��Ҫע�⣻���⣬�ڣ�3���������QH2��m�Ķ��κ����ǹؼ����������QB���ʱ��Ӧ��B�����꣮


 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
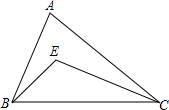 ��ͼ����ABC�У���ABC����ACB��ƽ�����ཻ�ڵ�E��
��ͼ����ABC�У���ABC����ACB��ƽ�����ཻ�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 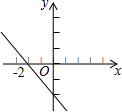 | B�� | 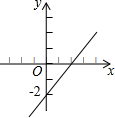 | C�� | 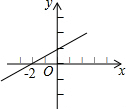 | D�� | 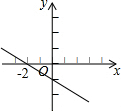 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ�����һ�β��ϣ��������֪ʶ������⣮
�Ķ�����һ�β��ϣ��������֪ʶ������⣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com