
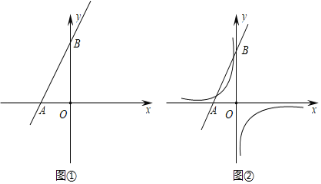
【题目】定义:两条长度相等,且它们所在的直线互相垂直,我们称这两条线段互为等垂线段.如图①,直线y=2x+4与x轴交于点A,与y轴交于点 B.
(1)若线段AB与线段BC互为等垂线段.求A、B、C的坐标.
(2)如图②,点D是反比例函数y=﹣![]() 的图象上任意一点,点E(m,1),线段DE与线段AB互为等垂线段,求m的值;
的图象上任意一点,点E(m,1),线段DE与线段AB互为等垂线段,求m的值;
(3)抛物线y=ax2+bx+c(a≠0)经过A、B两点.
①用含a的代数式表示b.
②点P为平面直角坐标系内的一点,在抛物线上存在点Q,使得线段PQ与线段AB互为等垂线段,且它们互相平分,请直接写出满足上述条件的a值.
【答案】(1)点A、B的坐标分别为(﹣2,0)、(0,4),点C(4,2);(2)m=![]() ;(3)①b=2a+2;②a=﹣
;(3)①b=2a+2;②a=﹣![]() .
.
【解析】
(1)证明△AOB≌△CDB(AAS),则BD=OA=2,DC=OB=4,即可求解;
(2)设点D(n,﹣![]() ),则点H(n﹣2,1),点E(n﹣2+4,﹣
),则点H(n﹣2,1),点E(n﹣2+4,﹣![]() ﹣2),而点E(m,1),即可求解;
﹣2),而点E(m,1),即可求解;
(3)①将点A、B的坐标代入二次函数表达式即可求解;②确定直线PQ的表达式为y=﹣![]() x+
x+![]() ,则点G(3,0),则HG=
,则点G(3,0),则HG=![]() =2
=2![]() ,而HQ=
,而HQ=![]() AB=
AB=![]() ,即点Q是HG的中点,求出点Q(1,1),将点A、B、Q的坐标代入二次函数表达式即可求解.
,即点Q是HG的中点,求出点Q(1,1),将点A、B、Q的坐标代入二次函数表达式即可求解.
(1)如图①,过点C作CD⊥y轴于点D,
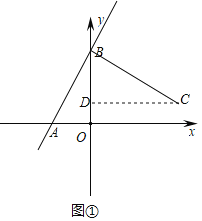
y=2x+4,令x=0,则y=4,令y=0,则x=﹣2,
故点A、B的坐标分别为(﹣2,0)、(0,4),
∵∠ABO+∠CBD=90°,∠ABO+∠BAO=90°,
∴∠BAO=∠DBC,
∠AOB=∠CDB=90°,AB=BC,
∴△AOB≌△CDB(AAS),
∴BD=OA=2,DC=OB=4,
∴点C(4,2);
(2)如图②,由(1)知,△AOB≌△EHD(AAS),

则HE=OB=4,DH=OA=2,
设点D(n,﹣),![]() 则点H(n﹣2,1),点E(n﹣2+4,﹣
则点H(n﹣2,1),点E(n﹣2+4,﹣![]() ﹣2),
﹣2),
而点E(m,1),
即:m=n+2;﹣![]() ﹣2=1,
﹣2=1,
解得:m=![]() ;
;
(3)①将点A、B的坐标代入二次函数表达式得:![]() ,
,
故:b=2a+2;
②如图③,PQ与BA交于点H,即点H是两条线段的中点,延长PQ交x轴于点G,
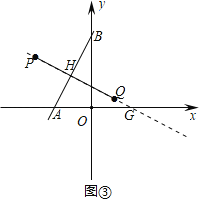
则点H(﹣1,2),直线AB表达式中的k值为2,则直线PQ表达式中的k值为﹣![]() ,
,
则直线PQ的表达式为:y=﹣![]() x+b,将点H坐标代入上式并解得:b=
x+b,将点H坐标代入上式并解得:b=![]() ,
,
则直线PQ的表达式为:y=﹣![]() x+
x+![]() ,
,
则点G(3,0),则HG=![]() =2
=2![]() ,而HQ=
,而HQ=![]() AB=
AB=![]() ,
,
即点Q是HG的中点,则点Q(1,1),
将点A、B、Q的坐标代入二次函数表达式并解得:a=﹣![]() .
.


科目:初中数学 来源: 题型:
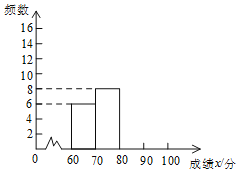
【题目】第十二届校园艺术节正在如火如荼的进行,我校九年级组织1500名学生参加了一次“湘一情校园知识”大赛.赛后发现所有参赛学生的成绩均不低于60分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中若干名学生的成绩作为样本,成绩如下:
90,92,81,82,78,95,86,88,72,66,62,68,89,86,93,97,100,73,76,80,77,81,86,89,82,85,71,68,74,98,90,97,100,84,87,73,65,92,96,60.
对上述成绩进行了整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
60≤x<70 | 6 | 0.15 |
70≤x<80 | 8 | 0.2 |
80≤x<90 | a | b |
90≤x≤100 | c | d |
请根据所给信息,解答下列问题:
(1)a= ,b= ,c= ,d= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,请你估计参加这次比赛的1500名学生中成绩“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
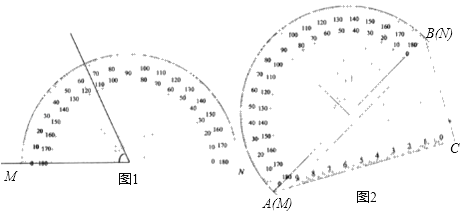
【题目】如图1,是用量角器一个角的操作示意图,量角器的读数从M点开始(即M点的读数为0),如图2,把这个量角器与一块30°(∠CAB=30°)角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有射线C绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB,在旋转过程中,射线CP与量角器的半圆弧交于E.连接BE.
(1)当射线CP经过AB的中点时,点E处的读数是 ,此时△BCE的形状是 ;
(2)设旋转x秒后,点E处的读数为y,求y与x的函数关系式;
(3)当CP旋转多少秒时,△BCE是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,BC=2AB,E,F分别是BC,AD的中点,AE,BF交于点O,连接EF,OC.
(1)求证:四边形ABEF是菱形;(2)若BC=8,∠ABC=60°,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个(记为A1,A2,A3),黑球2个(记为B1,B2).
(1)若先从袋中取出m(m>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:①若A为必然事件,则m的值为 ②若A为随机事件,则m的取值为
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用树状图或列表法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某爱心企业在政府的支持下投入资金,准备修建一批室外简易的足球场和篮球场,供市民免费使用,修建1个足球场和1个篮球场共需8.5万元,修建2个足球场和4个篮球场共需27万元.
(1)求修建一个足球场和一个篮球场各需多少万元?
(2)该企业预计修建这样的足球场和篮球场共20个,投入资金不超过90万元,求至少可以修建多少个足球场?
查看答案和解析>>
科目:初中数学 来源: 题型:
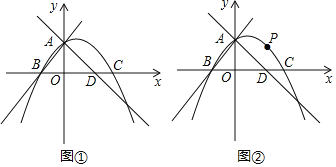
【题目】如图①,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,将直线
,将直线![]() 绕点
绕点![]() 逆时针旋转90°,所得直线与
逆时针旋转90°,所得直线与![]() 轴交于点
轴交于点![]() .
.
(1)求直线![]() 的函数解析式;
的函数解析式;
(2)如图②,若点![]() 是直线
是直线![]() 上方抛物线上的一个动点
上方抛物线上的一个动点
①当点![]() 到直线
到直线![]() 的距离最大时,求点
的距离最大时,求点![]() 的坐标和最大距离;
的坐标和最大距离;
②当点![]() 到直线
到直线![]() 的距离为
的距离为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
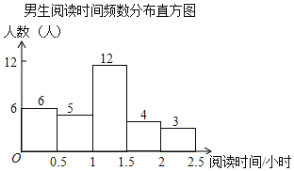
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正六边形ABCDEF的对称中心P在反比例函数![]() 的图象上,边CD在x轴上,点B在y轴上.已知
的图象上,边CD在x轴上,点B在y轴上.已知![]() .
.
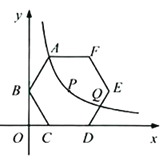
(1)点A是否在该反比例函数的图象上?请说明理由.
(2)若该反比例函数图象与DE交于点Q,求点Q的横坐标.
(3)平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com