
【题目】如图,![]() 的半径为
的半径为![]() ,
,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,连接
上一点,连接![]() 、
、![]() .
.![]() 为劣弧
为劣弧![]() 的中点,过点
的中点,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)连接![]() ,若
,若![]() ,如图2.
,如图2.
①求![]() 的长;
的长;
②图中阴影部分的面积等于_________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.


请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和m的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有1200名学生,根据抽查结果,估计该校学生在这一周内文章阅读的篇数为4篇的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器商场销售甲、乙两种品牌空调,已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20%,用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台.
(1)求甲、乙两种品牌空调的进货价;
(2)该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售,其中甲种品牌空调的售价为2500元/台,乙种品牌空调的售价为3500元/台.请您帮该商场设计一种进货方案,使得在售完这10台空调后获利最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里有四个完全相同的小球,把它们分别标号为![]() ,
,![]() ,
,![]() ,
,![]() .随机摸取一个小球然后放回,再随机摸取一个.
.随机摸取一个小球然后放回,再随机摸取一个.
请用画树状图和列表的方法,求下列事件的概率:
(1)两次取出的小球标号相同;
(2)两次取出的小球标号的和等于4.
查看答案和解析>>
科目:初中数学 来源: 题型:
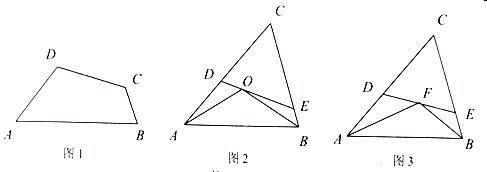
【题目】定义:有两个相邻内角和等于另两个内角和的一半的四边形称为半四边形,这两个角的夹边称为对半线.
(1)如图1,在对半四边形![]() 中,
中,![]() ,求
,求![]() 与
与![]() 的度数之和;
的度数之和;
(2)如图2,![]() 为锐角
为锐角![]() 的外心,过点
的外心,过点![]() 的直线交
的直线交![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,求证:四边形
,求证:四边形![]() 是对半四边形;
是对半四边形;
(3)如图3,在![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,当
,当![]() 为对半四边形
为对半四边形![]() 的对半线时,求
的对半线时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度y(m)与它的飞行时间x(s)满足二次函数关系,y与x的几组对应值如下表所示:
x(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(Ⅰ)求y关于x的函数解析式(不要求写x的取值范围);
(Ⅱ)问:小球的飞行高度能否达到22m?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等且非零的实数根,探究
有两个不相等且非零的实数根,探究![]() 满足的条件.
满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度研究一元二次方程的根的符号。下面是小华的探究过程:第一步:设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
第二步:借助二次函数图象,可以得到相应的一元二次方程中![]() 满足的条件,列表如下表。
满足的条件,列表如下表。
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
①_______ |
|
|
方程有两个不相等的正实根 | ② | ③____________ |
(1)请将表格中①②③补充完整;
(2)已知关于![]() 的方程
的方程![]() ,若方程的两根都是正数,求
,若方程的两根都是正数,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
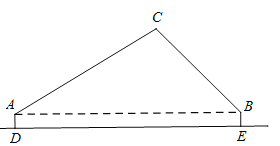
科目:初中数学 来源: 题型:
【题目】某数学小组在郊外的水平空地上对无人机进行测高实验.如图,两台测角仪分别放在A、B位置,且离地面高均为1米(即![]() 米),两台测角仪相距50米(即AB=50米).在某一时刻无人机位于点C (点C与点A、B在同一平面内),A处测得其仰角为
米),两台测角仪相距50米(即AB=50米).在某一时刻无人机位于点C (点C与点A、B在同一平面内),A处测得其仰角为![]() ,B处测得其仰角为
,B处测得其仰角为![]() .(参考数据:
.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
(1)求该时刻无人机的离地高度;(单位:米,结果保留整数)
(2)无人机沿水平方向向左飞行2秒后到达点F(点F与点A、B、C在同一平面内),此时于A处测得无人机的仰角为![]() ,求无人机水平飞行的平均速度.(单位:米/秒,结果保留整数)
,求无人机水平飞行的平均速度.(单位:米/秒,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
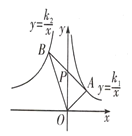
【题目】如图,点A、B分别在反比例函数y=![]() (k1>0) 和 y=
(k1>0) 和 y=![]() (k2<0)的图象上,连接AB交y轴于点P,且点A与点B关于P成中心对称.若△AOB的面积为4,则k1-k2=______.
(k2<0)的图象上,连接AB交y轴于点P,且点A与点B关于P成中心对称.若△AOB的面积为4,则k1-k2=______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com